Измерительные шкалы

Номинативная шкала (неметрическая), или шкала наименований (номинальное измерение). В ее основе лежит процедура, обычно не ассоциируемая с измерением. Пользуясь определенным правилом, объекты группируются по различным классам так, чтобы внутри класса они были идентичны по измеряемому свойству. Каждому классу дается наименование и обозначение, обычно числовое. Затем каждому объекту присваивается соответствующее обозначение.

Примеры номинативных признаков: пол (1 — мужской, 0 — женский), национальность (1 — русский, 2 — белорус, 3 — украинец), предпочтение домашних животных (1 — собаки, 2 — кошки, 3 — крысы, 0 — никакие) и т. д. В последнем случае если одному испытуемому присвоена 1, а другому 2, то это обозначает только то, что у них разные предпочтения: у первого — собаки, у второго — кошки. Из того, что 1 < 2, нельзя делать вывод, что у второго предпочтение выражено больше, чем у первого, и т.д.

В этом случае мы учитываем только одно свойство чисел — то, что это разные символы. Остальные свойства чисел не учитываются. Привычные операции с числами — упорядочивание, сложение-вычитание, деление — при измерении в номинативной шкале теряют смысл. При сравнении объектов мы можем делать вывод только о том, принадлежат они к одному или разным классам, тождественны или нет по измеренному свойству. Несмотря на такие ограничения, номинативные шкалы широко используются в психологии, и к ним применимы специальные процедуры обработки и анализа данных.

Ранговая, или порядковая шкала (неметрическая) (как результат ранжирования). Как следует из названия, измерение в этой шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства.

Пример. Мы можем ранжировать всех испытуемых по интересующему нас свойству на основе экспертной оценки или по результатам выполнения некоторого задания и приписать каждому испытуемому его ранг. Или предложить испытуемым самим определить выраженность изучаемого свойства, пользуясь предложенной шкалой (5-, 7- или 10-балльной).

Существует множество способов получения измерения в порядковой шкале. Но суть остается общей: при сравнении испытуемых друг с другом мы можем сказать, больше или меньше выражено свойство, но не можем сказать, насколько больше или насколько меньше оно выражено, а уж тем более — во сколько раз больше или меньше. При измерении в ранговой шкале, таким образом, из всех свойств чисел учитывается то, что они разные, и то, что одно число больше, чем другое.

Интервальная шкала (метрическая). Это такое измерение, при котором числа отражает не только различия между объектами в уровне выраженности свойства (характеристика порядковой шкалы), но и то, насколько больше или меньше выражено свойство. Равным разностям между числами в этой шкале соответствуют равные разности в уровне выраженности измеренного свойства. Иначе говоря, измерение в этой шкале предполагает возможность применения единицы измерения (метрики)

Главное понятие этой шкалы — интервал, который можно определить как долю или часть измеряемого свойства между двумя соседними позициями на шкале. Размер интервала — величина фиксированная и постоянная на всех участках шкалы. Для измерения посредством шкалы интервалов устанавливаются специальные единицы измерения; в психологии это стены и стенайны. При работе с этой шкалой измеряемому свойству или предмету присваивается число единиц измерения, пропорциональное выраженности измеряемого свойства.

Важная особенность интервальной шкалы — произвольность выбора нулевой точки: ноль вовсе не соответствует полному отсутствию измеряемого свойства. Произвольность выбора нулевой точки отсчета обозначает, что измерение в этой шкале не соответствует абсолютному количеству измеряемого свойства. Следовательно, применяя эту шкалу, мы можем судить, насколько больше или насколько меньше выражено свойство при сравнении объектов, но не можем судить о том, во сколько раз больше или меньше выражено свойство.

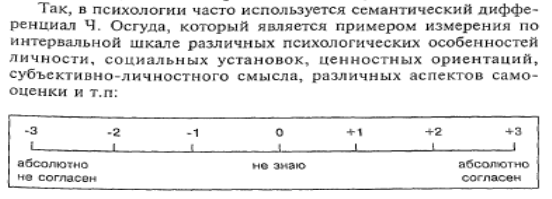
Интервальные измерения широко используются в психологии. Примеры: тестовые шкалы, которые специально вводятся при обосновании равноинтервальности (метричности) тестовой шкалы (IQ Векслера, стены и т.д.).

Только измерение по строго стандартизированной тестовой методике, при условии того, что распределение значений в репрезентативной выборке достаточно близко к нормальному (см. ниже), может считаться измерением в интервальной шкале.

Абсолютная шкала, или шкала отношений (метрическая). Измерение в этой шкале отличается от интервального только тем, что в ней устанавливается нулевая точка, соответствующая полному отсутствию выраженности измеряемого свойства.

В силу абсолютности нулевой точки, при сравнении объектов мы можем сказать не только о том, насколько больше или меньше выражено свойство, но и о том, во сколько раз (на сколько процентов и т. д.) больше или меньше оно выражено. Измерив время решения задачи парой испытуемых, мы можем сказать не только о том, кто и на сколько секунд (минут) решил задачу быстрее, но и о том, во сколько раз (на сколько процентов) быстрее.

Следует отметить, что, несмотря на привычность и обыденность абсолютной шкалы, в психологии она используется не часто. Из редких примеров можно привести измерение времени реакции (обычно в миллисекундах) и измерение абсолютных порогов чувствительности (в физических единицах свойств стимула).

Перечисленные шкалы полезно характеризовать еще и по признаку их дифференцирующей способности (мощности). В этом отношении шкалы по мере возрастания мощности располагаются следующим образом: номинативная, ранговая, интервальная, абсолютная. Таким образом, неметрические шкалы заведомо менее мощные — они отражают меньше информации о различии объектов (испытуемых) по измеренному свойству, и, напротив, метрические шкалы более мощные, они лучше дифференцируют испытуемых. Поэтому, если у исследователя есть возможность выбора, следует применить более мощную шкалу. Другое дело, что чаще такого выбора нет, и приходится использовать доступную измерительную шкалу. Более того, часто исследователю даже трудно определить, какую шкалу он применяет.

Правила ранжирования:

1. Правило порядка ранжирования. Вы можете ранжировать испытуемых по их месту в группе: ранг 1 присваивается тому, у которого наименьшая выраженность признака, и далее — увеличение ранга по мере увеличения уровня признака. Или можно ранг 1 присваивать тому, у которого 1-е место по выраженности данного признака (например, самый быстрый). Строгих правил выбора здесь нет, но важно помнить, в каком направлении производилось ранжирование.

2. Правило связанных рангов, когда двое или более испытуемых имеют одинаковую выраженность измеряемого свойства. Объектам с одинаковой выраженностью свойства приписывается один и тот же ранг. Этот ранг представляет собой среднее значение тех рангов, которые они получили бы, если бы не были равны.

Например, если вы ранжируете испытуемых по месту в группе и двое имеют одинаковые самые высокие исходные оценки, то обоим присваивается средний ранг 1,5: (1+2)/2 = 1,5. Следующему за этой парой испытуемому присваивается ранг 3 и т. д. Это правило основано на соглашении соблюдения одинаковой суммы рангов для связанных и несвязанных рангов. В соответствии с этим правилом сумма всех присвоенных рангов для группы численностью N должна равняться N(N+1)/2, вне зависимости от наличия или отсутствия связей в рангах