Раздел 5. Нормальное распределение. Проверка распределения на нормальность

Распределение Гаусса

Значения моды, медианы и среднего равны

Нормальный закон распределения играет важнейшую роль в применении численных методов в психологии. Он лежит в основе измерений, разработки тестовых шкал, методов проверки гипотез.

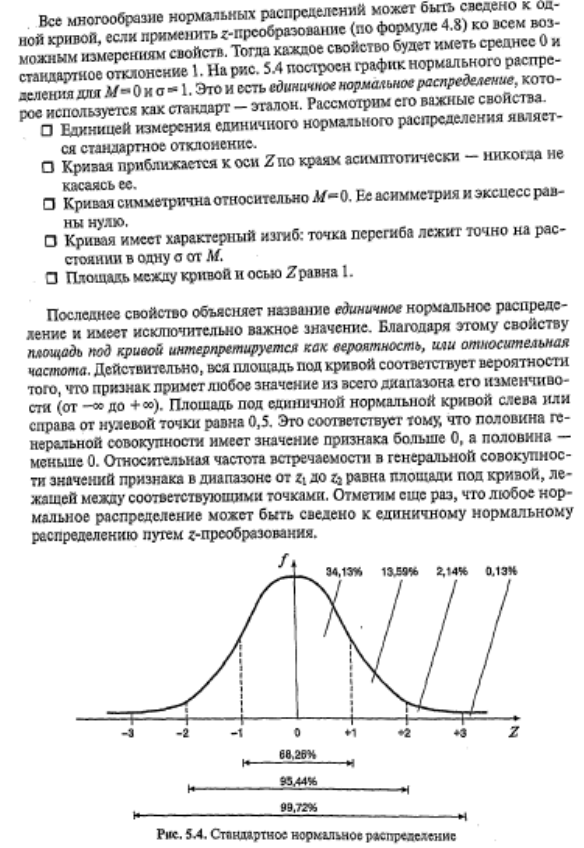
Для проверки нормальности распределения используются различные процедуры, позволяющие выяснить, отличается ли от нормального выборочное распределение измеренной переменной.

Критерии асимметрии и эксцесса.Эти критерии определяют допустимую степень отклонения эмпирических значений асимметрии иэксцесса от нулевых значений, соответствующих нормальному распределению. Допустимая степень отклонения — та, которая позволяет считать, что эти статистики существенно не отличаются от нормальных параметров. Величина допустимых отклонений определяется так называемыми стандартными ошибками асимметрии и эксцесса. Для формулы асимметрии (4.10) стандартная ошибка определяются по формуле:

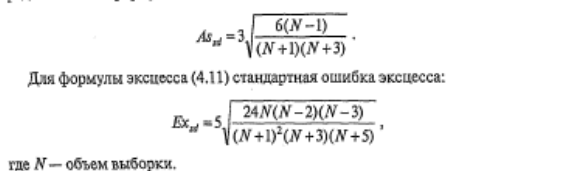
Выборочные значения асимметрии и эксцесса значительно отличаются от нуля, если не превышают значения своих стандартных ошибок. Это можно считать признаком соответствия выборочного распределения нормальному закону. Следует отметить, что компьютерные программы вычисляют показатели асимметрии, эксцесса и соответствующие им стандартные ошибки по другим, более сложным формулам.

Графический способ (Q-Q Plots, Р-Р Plots), Строят либо квантильные графики, либо графики накопленных частот. Квантильные графики (Q-Q Plots) строятся следующим образом. Сначала определяются эмпирические значения изучаемого признака, соответствующие5, 10,..., 95-процентилю. Затем по таблице нормального распределения для каждого из этих процентилей определяются г-значения (теоретические). Два полученных ряда чисел задают координаты точек на графике: эмпирические значения признака откладываются на оси абсцисс, а соответствующие им теоретические значения на ординат. Для нормального распределения все точки будут лежать на одной прямой или рядом с ней. Чем больше расстояние от точек до прямой линии, тем меньше распределение соответствует нормальному.

График накопленных частот (Р-Р Plots) строятся подобным образом. На оси абсцисс через равные интервалы откладываются значения накопленных относительных частот, например 0,05; 0,1;...; 0,95. Далее определяются эмпирические значения изучаемого признака, соответствующие каждому значению накопленной частоты, которые пересчитываются в z-значения. По таблице нормального распределения определяются теоретические накопленные частоты (площадь под кривой) для каждого из вычисленных z-значений, которые откладываются на оси ординат. Если распределение соответствует нормальному, полученные на графике точки лежат на одной прямой.

Статистический критерий нормальности Колмогорова-Смирновасчитается наиболее состоятельным для определения степени соответствия эмпирического распределения нормальному. Он позволяет оценить вероятность того, что данная выборка принадлежит генеральной совокупности с нормальным распределением. Если эта вероятность р< 0,05, то данное эмпирическое распределение существенно отличается от нормального, а если р > 0,05, то делают вывод о приблизительном соответствии данного эмпирического распределения нормальному.

Причины отклонения от нормальности.Общей причиной отклонения формы выборочного распределения признака от нормального вида чаще всего является особенность процедуры измерения: используемая шкала может обладать неравномерной чувствительностью к измеряемому свойству в разных частях диапазона его изменчивости.

Таким образом, такие отклонения от нормального вида, как право- или левосторонняя асимметрия или слишком большой эксцесс (больше 0), связаны с относительно низкой чувствительностью измерительной процедуры в области моды (вершины графика распределения частот).

Последствия отклонения от нормальности.Следует отметить, что задача получения эмпирического распределения, строго соответствующего нормальному закону, нечасто встречается в практике исследования. Обычно такие случаи ограничиваются разработкой новой измерительной процедуры или тестовой шкалы, когда применяется эмпирическая или нелинейная нормализация для исправления эмпирического распределения. В большинстве случаев соответствие или несоответствие нормальности является тем свойством измеренного признака, который исследователь должен учитывать при выборе статистических процедур анализа данных.

В общем случае при значительном отклонении эмпирического распределения от нормального следует отказаться от предположения о том, что признак измерен в метрической шкале.