Раздел 6. Корреляционный анализ
Корреляция – это согласованность изменений двух признаков.
Если два явления изменяются синхронно и эти изменения можно выразить количественно, что между показателями этих явлений будет наблюдаться корреляция. Например, корреляция может наблюдаться между ростом и весом людей (большая вероятность того, что чем выше человек, тем больше будет его вес). Или между уровнем интеллекта и показателями школьной успеваемости.
Нельзя говорить, что корреляция представляет собой выражение зависимости одного явления от другого, т.к. она не всегда предполагает наличие причинно-следственной связи.
Степень связи между признаками выражается величиной, называемой коэффициентом корреляции.
Коэффициент корреляции— двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.
Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий. На рис. 6.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.

Функциональные связи,подобные изображенным на рис. 6.1, являются идеализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной.
Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.
В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков.
Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная: одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной - идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых.
Итак, в психологии, как и во многих других науках, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания - график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рис. 6.2).
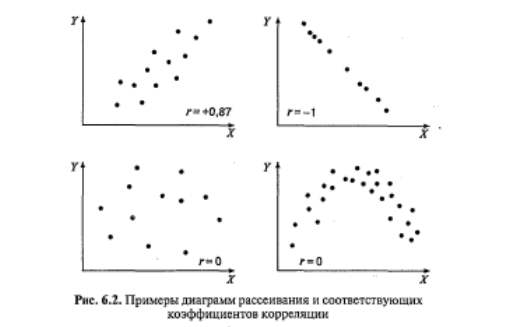
Значения коэффициента корреляции (R или r) могут находиться в диапазоне от от –1 до +1.
Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью.
Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции (значение коэффициента корреляции приближается к единице).
Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной).
Если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.
Величина, близкая к нулю, говорит об отсутствии выявленной взаимосвязи между признаками.
Классификация коэффициентов корреляции по силе:
| Сильная | r > 0,70 |
| Средняя | 0,50 < r < 0,69 |
| Умеренная | 0,30 < r < 0,49 |
| Слабая | 0,20 < r < 0,29 |
| Очень слабая | r < 0,19 |
Классификация коэффициентов корреляции по значимости:
| Высокозначимая корреляция | r соответствует p≤0,01 |
| Статистически значимая корреляция | r соответствует p≤0,05 |
| Незначимая корреляция | r не достигает p>0,1 |
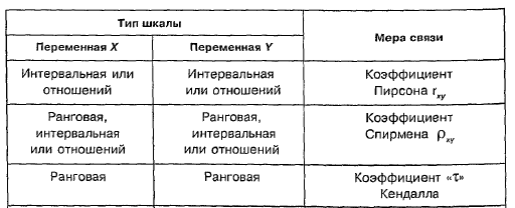
В зависимости от типа шкалы, в которой измерены переменные, используют различные виды корреляции: линейную (метрическую), ранговую и между номинативными переменными.
Измерение в метрических шкалах и укладываются в кривую нормального распределения – коэф. кор. Пирсона.
Распределение отличается от нормального – преобразование метрических данных в ранговые (либо порядковая шкала) – коэф. кор. Спирмена, Кендалла.
Зависимости номинативных переменных – С-Пирсона, хи-квадрат Пирсона, точный критерий Фишера, статистику фи-квадрат.
Дата добавления: 2016-03-04; просмотров: 1054;
