Меры центральной тенденции
Мера центральной тенденции (Central Tendency) — это число, характеризующее выборку по уровню выраженности измеренного признака.
Существуют три способа определения центральной тенденции, каждому из которых соответствует своя мера: мода, медиана и выборочное среднее.
Мода (Mode) — наиболее часто встречающееся значение в ряду данных. Моде, или модальному интервалу признака, соответствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.
Среди 8 значений признака (3, 7, 3, 5, 7, 8, 7, 6) мода Мо=7 как наиболее часто встречающееся значение.
Когда два соседних значения встречаются одинаково часто и чаще, чем любое другое значение, мода есть среднее этих двух значений.
Распределение может иметь и не одну моду. Когда все значения встречаются одинаково часто, принято считать, что такое распределение не имеет моды.
Бимодальное распределение имеет на графике распределения две вершины, даже если частоты для двух вершин не строго равны. В последнем случае выделяют большую и меньшую моду. Во всей группе может быть и несколько локальных вершин распределения частот. Тогда выделяют наибольшую моду и локальные моды.
Бимодальное, полимодальное распределение может рассматриваться как признак неоднородности выборки. Например, механическое слияние двух классов с неодинаковым уровнем интеллекта.
Еще раз отметим, что мода — это значение признака, а не его частота.
Медиана (Median) — это такое значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так, что одна половина всех значений оказывается меньше медианы, а другая — больше. Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:
• если данные содержат нечетное число значений (8, 9,10,13,15), то медиана есть центральное значение, т. е. Md = 10;
• если данные содержат четное число значений (5, 8, 9, 11), то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Md= (8+9)/2=8,5.
Среднее(Mean) (Мх — выборочное среднее, среднее арифметическое) — определяется как сумма всех значений измеренного признака, деленная на количество суммированных значений.


Наиболее очевидной и часто используемой мерой центральной тенденции является среднее значение. Но его использование ограничивается тем, что на величину среднего влияет каждое отдельное значение. Если какое-нибудь значение в группе увеличится на с, то среднее увеличится на c/N. Таким образом, среднее значение весьма чувствительно к выбросам — экстремально малым или большим значениям переменной.
Меры изменчивости
Меры центральной тенденции отражают уровень выраженности измеренного признака. Однако не менее важной характеристикой является выраженность индивидуальных различий испытуемых по измеренному признаку. Меры изменчивости (Dispersion) применяются в психологии для численного выражения величины межиндивидуальной вариации признака.
Наиболее простой и очевидной мерой изменчивости является размах, указывающий на диапазон изменчивости значений. Размах (Range) — это просто разность максимального и минимального значений:
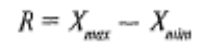
Для определение размаха выборку необходимо сначала упорядочить.
Ясно, что это очень неустойчивая мера изменчивости, на которую влияют любые возможные выбросы.

Для метрических данных используется дисперсия — величина, название которой в науке является синонимом изменчивости.
Дисперсия (Variance) — мера изменчивости данных относительно среднего значения.
Мера изменчивости для метрических данных, пропорциональная сумме квадратов отклонений измеренных значений от их арифметического среднего:
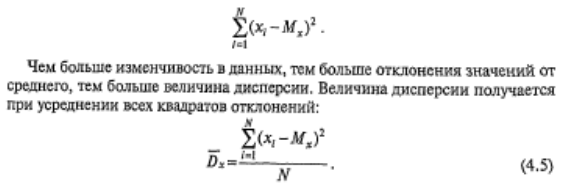


Дата добавления: 2016-03-04; просмотров: 1903;
