Аксиомы, законы, тождества и теоремы алгебры логики. В алгебре логики любая переменная может иметь состояние «О» или «1»
В алгебре логики любая переменная может иметь состояние «О» или «1». Поэтому в алгебре логики каждой двоичной переменной, например х, ставится в соответствие обратная или дополнительная к ней (инверсная) переменная, такая, что:
если х = 0, то `x = 1, если х = 1, то `х = 0.
Переменную `х следует читать как НЕ х.
В алгебре логики в случае одной переменной х действуют следующие правила (аксиомы):
1) x + 0 = х, 6) х • 0 = О,
2) х+ 1 = 1, 7) х • 1 =х,
3) х + х = х, 8) х • х = х, (3.55)
4) х +` х = 1, 9) х •`х = 0, __
5) (`х) = `х, 10) ` ( х)=`х.
Правила 1—4 характеризуют операцию логического сложения (дизъюнкции), правила 6—9 — операцию логического умножения (конъюнкции) и правила 5,10 — операцию инверсии. Знак логического сложения «+» читается ИЛИ (например, правило 1 : «х или 0 равен x»). Знак логического умножения «•» читается И (например, «x и 0 равен 0»).
Правила 1—4, 6—9 поясняются схемами (рис. 3.19, а — з) на двух ключах в соответствии с числом слагаемых (сомножителей) в соотношениях. Положению «Ключ включен» соответствует состояние «1», а положению «Ключ выключен» — состояние «О». Для логического сложения (правила 1—4) ключи в схемах соединены параллельно. Уровень высокого напряжения на выходе (F = 1) будет иметь место, если хотя бы один ключ находится в состоянии «1» (правила 2, 4; рис. 3.19, б, г). Результат суммы в правилах 1, 3 зависит от значения х
(при х = 1 F = 1, при х = 0 F = 0; рис. 3.19, а, в). Для логического умножения ключи соединены последовательно (рис. 3.19, д — з). Уровень высокого напряжения на выходе (F = 1) будет только в том случае, если оба сомножителя равны единице (оба ключа включены). В противном случае результат умножения равен нулю (правила 6, 9; рис. 3.19, д, з). Результат умножения в правилах 7, 8 зависит от значения х (рис. 3.19, е,ж).
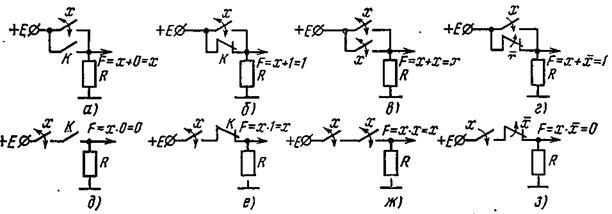
Рис. 3.19. Схемы, иллюстрирующие операции логического сложения (а — г)
и логического умножения (д — з)
Для алгебры логики, как и для обычной алгебры, действительны следующие законы.
Переместительный закон (закон коммутативности) для логического сложения и умножения:
1 ) x + y = y + x (3.56)
2) х • у = у • х.
Сочетательный закон (закон ассоциативности) для логического сложения и умножения:
1) x+ у+г=(х + у)+г = х+(у + г),
2) х • у • z = (x • у) • г = х(у • г).
Распределительный закон (закон дистрибутивности логического умножения по отношению к сложению):
х (у + z) = ху + хг. (3.58)
Для многих случаев алгебраических преобразований полезными являются тождества, относящиеся к двум и трем переменным:
1) ху + х`у = х, 4) х (`х + у) = xy
2) х + ху = х, 5) (х + у) (х + z) = х + уг,
3) х (х + у)=х, 6) х`у + у = х + у. (3.59)
В справедливости тождеств 1 и 2 нетрудно убедиться, вынося за скобку в левой части переменную х. Тождество 3 доказывается с помощью распределительного закона х(х + у) = хх + ху = х + ху =
= х. Аналогично доказывается и тождество 4. Для доказательства тождества 5 раскроем скобки в левой части: (х + у)(х + z) = х + + xz + ху + уг = х + ху + yz = х + yz.
К основным законам алгебры логики относятся законы инверсии для логических сложения и умножения (теоремы де Моргана):
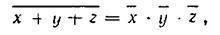 (3.60) (3.60)
|
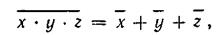 (З.60а) (З.60а)
|
т. е. инверсия суммы переменных есть произведение их инверсий;
т. е. инверсия произведения переменных есть сумма их инверсий.
Справедливость соотношений (3.60) и (З.60а) для двух переменных подтверждает табл. 3.1.
Таблица 3.1
| x | y | `х | `у | x + у | x • у | _____ x + y | `x •`у | ____ x • y | `x +`y |
| 0 0 1 1 | 1 0 | 1 1 0 0 | 1 0 | 111 1 |
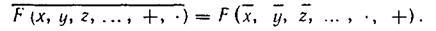 (3.61) (3.61)
|
В общем случае теоремы де Моргана могут быть представлены в виде, предложенном Шенноном:
Теорема в таком виде утверждает, что инверсия любой функции получается заменой каждой переменной ее инверсией и одновременно взаимной заменой символов сложения и умножения. При практическом применении теоремы необходимо строго соблюдать группировки членов, выраженные как явными, так и неявными скобками. В качестве примера определим инверсию функции
F = х`у + x`y. По правилу (3.61) находим
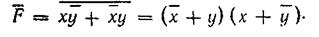
Понятия инверсии и инверсного преобразования играют важную роль при синтезе схем. Использование инверсии на определенном этапе синтеза, в частности, приводит иногда к существенному упрощению функции, а следовательно, и средств ее реализации.
Логические функции
Логическая функция может быть записана аналитически различными сочетаниями операций сложения и умножения переменных. Однако с точки зрения представления логической функции и после-
дующего синтеза логической схемы наиболее удобны формы записи, при которых функция выражается либо в виде суммы произведений переменных, либо в виде произведения их сумм.
Запись логической функции в виде суммы произведений переменных называют дизъюнктивной нормальной ф о р м о й (ДНФ):
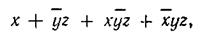
|
а запись функции в виде произведения сумм — конъюнктивной нормальной формой (КНФ):
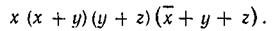
|
Инверсия любой функции, записанной в дизъюнктивной (конъюнктивной) нормальной форме, по правилу (3.61) дает замену записи на конъюнктивную (дизъюнктивную) нормальную форму. Например, инверсия функции
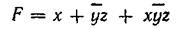
имеет вид
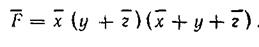
Логическую функцию, заданную любым аналитическим выражением, можно преобразовать к ДНФ или КНФ, пользуясь правилами алгебры логики. Для каждой логической функции может существовать несколько равносильных дизъюнктивных и конъюнктивных форм.
Вместе с тем имеется только один вид ДНФ и КНФ, в которых функция может быть записана единственным образом (совершенные нормальные форм ы). В совершенной дизъюнктивной нормальной форме (СДНФ) каждое входящее слагаемое включает все переменные .(с инверсиями и без них) и нет одинаковых слагаемых. В совершенной конъюнктивной нормальной форме (СКНФ) каждый входящий сомножитель включает все переменные (с инверсиями и без них) и нет одинаковых сомножителей.
Логическая функция наиболее наглядно и полно представляется так называемой таблицей соответствия или истинности, в которой для каждой комбинации значений переменных указывается значение функции. Таким образом, таблица истинности определяет алгоритм работы создаваемой цифровой схемы. От табличного представления функции переходят к аналитической записи ее в СДНФ или СКНФ.
Пусть в качестве примера функция F задана в виде табл. 3.2. Для комбинаций переменных 2, 7, 8 функция F истинна (т. е. F = 1), что означает для указанных комбинаций равенство единице следующих произведений: `x`y z = 1, х у`z = 1 и хуz = 1. Комбинации переменных,
Таблица 3.2
| Номер комбинации | x | у | z | F |
| 0 0 0 0 1 1 1 | 0 0 1 1 0 0 1 1 | 0 0 0 0 1 1 |
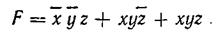
|
при которых функция истинна, называют конституентами единицы или минтермами. Представление логической функции в виде суммы минтермов определяет ее СДНФ, т. е. в данном случае
(3.62)
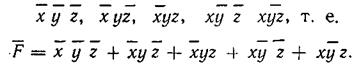 (3.63) (3.63)
|
Функция, определяемая таблицей истинности, может быть представлена не только ее единичными, но и нулевыми значениями. Так, на основании табл. 3.2 рассматриваемая функция ложна (F = 0 или `F = 1), если истинно каждое из произведений
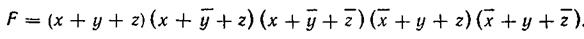 (3.64) (3.64)
|
Воспользовавшись законом инверсии, приходим к записи функции в СКНФ:
Каждый сомножитель в соотношении (3.64) состоит из суммы переменных, для которых функция обращается в нуль в соответствии с таблицей истинности. Такие суммы называют конституентам и нуля или макстермами. Таким образом, произведение макстермов определяет СКНФ функции.
Дата добавления: 2016-04-06; просмотров: 1982;
