Алгебры и алгебры множеств.
Некоторые сведения из математики.
При построении вероятностных моделей для экспериментов с несчетным числом исходов возникают определенные трудности, но прежде чем рассматривать пути преодоления этих трудностей и изучать системы аксиом теории вероятностей, изложим некоторые сведения из теории множеств и теории меры, которые в дальнейшем будут играть существенную роль.
Будем рассматривать некоторое множество Ω и подмножества этого множества.
Определение. Класс U подмножеств из Ω называется алгеброй, если:
1) 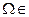 U;
U;
2) из того, что 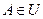 , следует, что
, следует, что 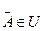 ;
;
3) из того, что 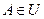 ,
, 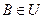 , следует, что
, следует, что 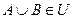 .
.
Замечание. Если U-алгебра, то из того, что 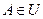 ,
, 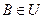 , следует А∩В
, следует А∩В
принадлежит А.
Действительно, 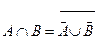 .
.
ПРИМЕРЫ
1. Пусть А — некоторое подмножество Ω, Тогда класс множеств
U = {Ω, Ø,A, Ā}
образует алгебру.
2. Пусть Ω=[0,1) и U — система подмножеств из Ω, каждое из которых представляет собой конечную сумму непересекающихся интервалов вида [а, b). Тогда U — алгебра.
3. Пусть Ω= [0,1) 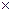 [0,1) и U—множество всех прямоугольников [а1 b1,)
[0,1) и U—множество всех прямоугольников [а1 b1,) 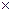 [a2, b2] и конечных сумм таких непересекающихся прямоугольников. Тогда U-алгебра.
[a2, b2] и конечных сумм таких непересекающихся прямоугольников. Тогда U-алгебра.
Определение. Класс F множеств из Ω, называется σ-алгеброй, если:
1) 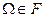 ;
;
2) из того, что 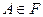 , следует
, следует 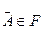 ;
;
3) из того, что 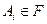 (i=1,2, ...), следует, что
(i=1,2, ...), следует, что
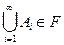 .
.
Пример: Множество всех подмножеств множества Ω образует σ – алгебру.
Основные понятия комбинаторики
Комбинаторика — это раздел математики, изучающий расположения объектов в соответствии со специальными правилами и методы подсчета числа всех возможных способов, которыми эти расположения могут быть сделаны.
Теорема умножения.
Пусть некоторое первое действие можно выполнить 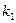 способом, второе действие -
способом, второе действие - 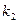 способом, ..., n – тое действие -
способом, ..., n – тое действие - 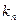 способом. Тогда все эти действия вместе можно выполнить
способом. Тогда все эти действия вместе можно выполнить 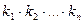 способом.
способом.
Пример:
Игральную кость бросают 3 раза. Сколько различных комбинаций очков можно при этом получить.
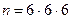
Дата добавления: 2016-02-27; просмотров: 1158;
