Условные вероятности
В ряде случаев приходится рассматривать вероятности случайных событий, если известно, что произошло некоторое случайное событие B, имеющее положительную вероятность. Прежде чем давать точное определение условной вероятности, рассмотрим несколько примеров.
ПРИМЕРЫ
1. Пусть дважды брошена симметричная игральная кость. В—событие, состоящее в том, что сумма появившихся очков меньше 4, а A— событие, состоящее в том, что первый раз появилась 1. Вычислим условную вероятность Ρ (А/В) события A, если известно, что произошло событие В.
Пространство элементарных событий состоит из 36 исходов:
Ω = {(i,j):i=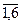 
,j= }.
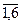События А и В — это следующие подмножества Ω:
A = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)};
В = {(1, 1), (1, 2), (2, 1)}.
Заметим, что
AÇB={(1,1),(1,2)}.
Поэтому
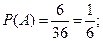
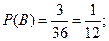
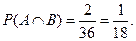
Если известно, что событие В произошло, то событие A могло произойти лишь тогда, когда произошло одно из элементарных событий (1, 1) или (1, 2). Поэтому естественно считать, что
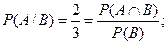
2. Предположим, что пространство элементарных событий Ω состоит из n одинаково возможных элементарных событий, событию A благоприятствует т элементарных событий, β состоит из l исходов, событию АÇВ благоприятствует r исходов. Найдем Ρ (А/В).
Заметим, что 
Если произошло событие B, то произошло одно из l элементарных событий; событие Л произойдет только тогда, когда произойдет одно из r элементарных событий, составляющих AÇ В. Поэтому
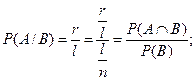
3. Пусть в квадрат Ω = [0, 1]2 наудачу бросают точку. Вероятность попадания во множество A равна m (А), где m (A) — площадь A.
Если мы интересуемся вероятностью Ρ (A/B) того, что точка попадает во множество A, при дополнительном предположении, что точка попадает во множество В, то естественно, считать, что вероятность Ρ (A/B) пропорциональна Ρ (A Ç B), т. е.
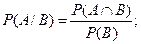
Определение. Пусть (Ω, F, Р)—вероятностное пространство, Ρ(B)>0, BÎF. Условной вероятностью события А при условии, что произошло событие В, называют
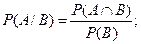
Из этого определения и свойств вероятности непосредственно
следует, что:
1) Р(A/B)³ 0;
2) Ρ(Ω/B)= 1;
3) Ρ (B/B)= 1,
4) если {Ai}— последовательность попарно несовместных случайных событий (Αi Ç Aj =Æ), то
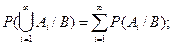
Докажем 2) и 4). Имеем:
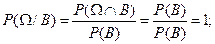
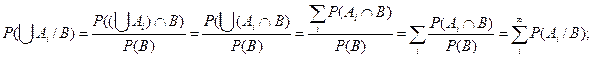
Заметим также, что Ρ(B/B) = 1. Обозначим через F δ-алгебру всех множеств вида А Ç В, где AÌF. Из свойств 1) — 4) следует что (В, Fв, Ρ (× /В)) — вероятностное пространство.
Соотношение (1) можно записать в виде Ρ (Α Ç В) = Ρ (Β) Ρ (А/В). Если Р(A)>0, то можно записать, что Ρ (А Ç В) = Ρ (A) Ρ (В/A). Итак, имеет место следующее утверждение.
Теорема 1. Если Р(B)>0, Р(A)>0, то имеют место равенства
Ρ (А Ç В) = Ρ (Β) Ρ (Α/В) = Ρ (A) Ρ (Β/Α). (2)
Соотношение (2) называют формулой умножения. Формула (2) допускает следующее обобщение.
Пусть A1.....,An — случайные события такие, что Р(А1Ç
Ç A2 Ç · · · Ç Ап-1) > 0. Поскольку
то из неравенства Р(А1Ç …ÇAn-1) > 0 следует, что
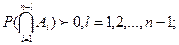
Следовательно, все условные вероятности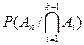 
определены.
Легко проверить (можно воспользоваться методом математической индукции), что
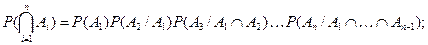(3)
Дата добавления: 2016-02-27; просмотров: 537;