Функция распределения случайной величины x(w) имеет вид

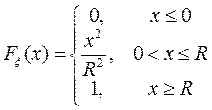
5. Пусть (W, f, P) — произвольное вероятностное пространство. Пред­положим, что А — некоторое случайное событие (А Î f) и

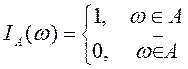
Заметим, что

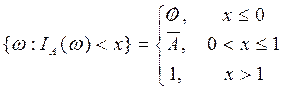
и, следовательно, множество {w : x(w) < x} Î f.

Итак, x(w) — случайная величина, функция распределения которой равна

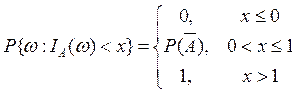
Случайную величину I_A(w) называют индикатором случайного события А. Рассмотрим еще пример вероятностного пространства и функции на нем, не являющейся случайной величиной.

6. Пусть W = [0, 1], U есть s-алгебра измеримых по Лебегу множеств из [О, 1]. Положим Р (А) = m(A), если А Î U, где m(А) — мера Лебега множества А. Тогда (W, U, Р) —вероятностное пространство.

Предположим, что Е — неизмеримое по Лебегу множество из отрезка [О, I]¹. Рассмотрим функцию

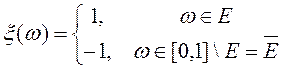
Тогда

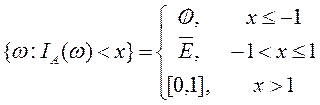
Следовательно, при –1 < x £ 1 {w:x(w)<x}=E Î U и функция x(w) не является случайной величиной на вероятностном пространстве (W, U, P).

Случайные события, порожденные случайной величиной или системой случайных величин.

Пусть x(w) – случайная величина, т. е. функция x(w):W®R = (-¥, +¥) измеримая относительно s-алгебры f. Предположим, что В – некоторое множество на числовой прямой. Рассмотрим множество

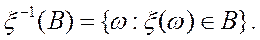
Является ли это множество случайным событием? Иначе говоря, можем ли мы утверждать, что

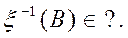
Если В = (- ¥, х), то по соотношению (1) из определения слу­чайной величины x^-1((-¥, x))={w:x(w)<x}Îf. Отсюда уже автоматически следует, что x^-1(B)Îf для довольно широкого класса множеств {В}.

Теорема 1. Пусть (W, f, P) — вероятностное пространство и x(w) — случайная величина на нем. Тогда каждое из множеств множества W

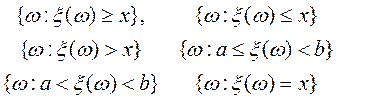
является случайным событием, т. е. каждое из этих множеств принадлежит s-алгебре f.

Теорема 4. Пусть (W, f, P) — вероятностное пространство, a x(w) и h(w) - случайные величины на нем. Тогда

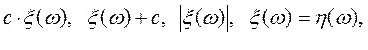
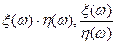- также случайные величины (в последнем случае предполагается, что Р{w:h(w)¹0} = 1).

Для доказательства теоремы достаточно заметить, что

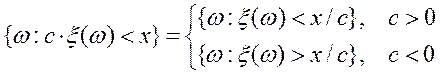
ПРИМЕРЫ

1. Пусть (W, f, P) — произвольное вероятностное пространство и x(w) = c для каждого w из W. Тогда x(w) — случайная величина. В самом деле,

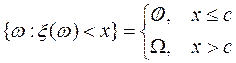
и при каждом действительном x{w : x(w) < x}Îf.

2. Пусть W — некоторое пространство, а f — система всех подмножеств W. Тогда каждая функция x(w) на W является случайной величиной.

Если f = {W, Æ} (это самая «тощая» s-алгебра подмножеств в W), то случайными величинами могут быть только константы.