Независимые случайные события

Ο п ρ е д е л е н и е. Пусть (Ω, F, Р) — вероятностное прост­ранство. Случайные события А и В (ΑÎF,BÎF) называются независимыми, если

ПРИМЕРЫ

1. Монету бросают дважды. Тогда Ω = {ΓΓ, ГР, РГ, РР}. Пусть А — событие, состоящее в том, что первый раз выпал герб, В — событие, состоя­щее в том, что второй раз выпал герб. Тогда

1-й

А = {ГГ, ГР}; В = {ГГ, ΡΓ}; AÇB ={ГГ};

и P(A)= 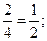P(B)= 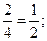P(AÇB)= ;

Итак, Р (А Ç В) = Р (A) Р (В). Следовательно, случайные события А и В неза­висимы.

2. Предположим, что в квадрат Ω = [0, 1 ]² наугад бросают точку. Пусть

F есть σ-алгебра всех борелевских множеств. из Ω, и если ΑÎ F, то Р (A) = m(A), где т (А) — площадь множества А. Мы рассматриваем «геометриче­ские вероятности». Пусть А — событие, состоящее в том, что абсцисса брошенной точки не меньше а, 0<а< 1, а В — событие, состоящее в том, что

ордината брошенной точки не меньше b, 0 < b < 1.

Тогда (рис. 7)

P(A)=1-a; P(B)=1-b;

P(A Ç B)=(1-a)(1-b)

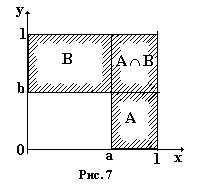
и,следовательно, события А и В независимы.

Рассмотрим некоторые простые, но важныесвойства независимых событий.

Теорема 1. Пусть Р(В) >0. Случайные события А и В независимы тогда итолько тогда, когда Р (А/В) = Р (А) (появление события В не изменяет вероятности события А).

Действительно, если А и В независимы и Ρ(В) > 0, то Если же известно, что

, а это означает, что А и В независимы.

Теорема 2. Если А и В независимы, то события А и `В, `А и`В также независимы.

Достаточно доказать, что А и В независимы. Заметим, что

А Ç`В = А\(А Ç В). Поэтому

Ρ (АÇ В) = Ρ (А) —Ρ (АÇВ).

Лекция 4

Случайные величины

Случайные величины — функции на пространстве элементар­ных событий. Одним из основных понятий теории вероятностей является понятие случайной величин ы. Случайная величина — это величина, принимающая те или иные значения, в за­висимости от случая. Примерами случайных величин могут быть число очков, выпадающих при одном бросании игральной кости, число бракованных изделий среди взятых наудачу п изделий, число попаданий в цель при п выстрелах, время безотказной работы при­бора, дальность полета баллистической ракеты и т. д. Случайная величина x есть число, которое ставится в соответствие каждому воз­можному исходу эксперимента. Поскольку исходы эксперимента описываются элементарными событиями, случайную величину мож­но рассматривать как функцию x = x(w) на пространстве элемен­тарных событий W.

Прежде чем давать определение случайной величины, рассмот­рим несколько примеров.

ПРИМЕРЫ

1. Пусть дважды бросают монету. Пространство элементарных событии имеет вид

W = {ГГ, ГР, РГ, РР}.

Пусть x — число появлений герба. Величина x является функцией x = x(w) элементарного события. Таблица значении функции x(w) имеет следующий вид:

2. Бросают игральную кость.

В этом случаи пространство элементарных событий имеет вид

где w_t означает, что выпало i очков. Случайная величина x — число появив­шихся очков — является функцией элементарного события, причем x(w) = i если w = w_i.

3. Монету бросают до тех пор, пока не появится герб. В этом случае

Пусть x — число бросаний. Тогда величина x является функцией элементар­ного события, причем x(w) = п, если w = w_n (п = 1 , 2, . . .).

Определение случайной величины. Рассмотренные примеры подтверждают, что случайные величины можно интерпретировать как функции на пространстве элементарных событий стохастичес­кого эксперимента. Однако не любые функции, определенные на W, можно рассматривать в качестве случайных величин. При изуче­нии величин часто придется отвечать на вопрос: какова вероят­ность того, что значения случайной величины x(w) принадлежат тому или иному множеству. Следовательно, для достаточно широ­кого класса множеств {В} на числовой прямой должна быть уверен­ность, что множество

{w:x(w)ÎB} принадлежит d-алгебре f случайных событий, и поэтому можно рассматривать вероятность P{w:x(w)ÎB}. Оказывается (в этом убедимся ниже), достаточно предположить, что для каждого интервала (-¥,x) множество{w:x(w)Î(-¥,x)}={w:x(w)<x}принадлежит d-алгебре f случайных событий, и тогда для каждого борелевского множества В получим{w:x(w)ÎB}Îf.

Определение.Пусть (W, f, P) - вероятностное про­странство. Всякая действительная функция x = x (w) на W такая, что для каждого действительного х

{w :x(w) < x}Îf (1)