Распределения случайных величин

Дискретные случайные величины. Пусть (W, f, P) — вероят­ностное пространство. Случайная величина x(w) называется дискретной случайной величиной, если она при­нимает конечное или счетное число значений.

Если x(w) — дискретная случайная величина на вероятностном пространстве (W, f, P), принимающая значения x₁,…,x_n,…, то для каждого n определена вероятность

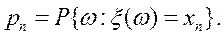(2)
Набор вероятностей (2) называется распределением
случайной величины x(w).

Распределение дискретной случайной величины удобно характе­ризовать с помощью следующей таблицы:

Заметим, что р_п ³ 0,

Непрерывные случайные величины

Плотность распределения случайной величины.

Пусть ξ — слу­чайная величина с функцией распределения F (х). Говорят, что слу­чайная величина имеет плотность распределения, если существует интегрируемая борелевская функция р (и) такая, что для всех х выполнимо равенство

F(x)= p (u)du. (10)

Функция р (х) называется плотностью распределе­ния случайной величины ξ.

Свойства плотности распределения

1.

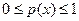
2.