Отметим следующие важные свойства функций распределения
а). Если a < b, то
P{w: a £ x(w) < b} = F(b) – F(a). (9)
б). Если a < b , то F(a)£F(b), т. е. F(x) – неубывающая функция.
в). 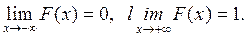
г). F(x) непрерывна слева.
д). P(w:x(w) £ x) = F(x + 0).
е). P{w:x(w) = x} = F(x + 0) - F(x).
Рассмотрим несколько примеров случайных величин.
1. Пусть один раз бросают симметричную монету.
В этом случаи W={w1,w2} где w1=Г, w2=Р; f – совокупность всех подмножеств W; Р({w1})=P({w2})=1/2. Предположим, что

Заметим, что

Таким образом, x(w) – случайная величина и

График функции распределения изображен на рис. 8.
2. Равномерное распределение на отрезке [a, b]. На отрезок [a, b] числовой прямой наугад бросают точку, причем считают, что все положения точки «одинаково возможны».
В рассматриваемом стохастическом эксперименте W = [a, b], f – есть s-алгебра борелевских подмножеств из [a, b], P(·) – такая мера на f, что P{[a, b)=(b-a)/(b-a), если [a, b)Ì[a, b]. Определим случайную величину x следующим образом: x(w) = w, если wÎ[a, b], т. е. x - координата полученной точки. Заметим, что
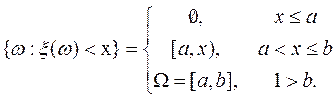
Таким образом, при каждом x{w:x(w<x)}Î f, т. е. x(w) – случайная величина. Функция распределения случайной величины x(w) имеет вид

Эта функция распределения (рис.9) определяет так называемое равномерное распределение на [a, b].
3. Задача о встрече.Два лица А и В условились о встрече на интервале времени [0, T].
Пусть u – время прихода А, v – время прихода В. Пространство элементарных событий имеет вид
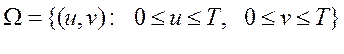
(см. пример 3, с. 4). В качестве s-алгебры f случайных событий рассмотрим s-алгебру измеримых по Борелю подмножеств квадрата [0, T]x[0, T]. Если СÎ f, то Р(С) =m(C)/T2, где m(С) — площадь множества С. Пусть x — время ожидания. Тогда x(w) = | u- v½, если w = (u, v). Заметим, что

Следовательно, функция x(w) измерима относительно s-алгебры f. Функция распределения x(w) равна

График функции распределения изображен на рис. 10.

|
4. Предположим, что в круг КR радиуса R с центром в начале координат наугад бросают точку. Пусть x — расстояние от точки до начала координат.
Пространство элементарных событий рассматриваемого эксперимента имеет вид
Рис. 10.
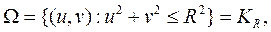
причем 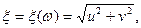 если w = (u, v).
если w = (u, v).
Пусть f есть s-алгебра борелевских множеств из КR. Функция x(w) измерима относительно f, так как множество

при каждом x принадлежит s-алгебре f. Если АÎf , то
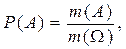
где m(·) — «площадь»множества А.
Дата добавления: 2016-02-27; просмотров: 580;
