Формула полной вероятности. Определение. Говорят, что набор случайных событий H1, ,Hn образует полную группу событий, если:
Определение. Говорят, что набор случайных событий H1,…,Hn образует полную группу событий, если:
1) H1ÈH2È…ÈHn= Ω; (4)
2) HiÇ Hj =Æ (i¹j).
Теорема 2. Если H1 ... ,Hn— полная группа событий и Ρ (Hi) > 0,i= 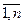 то для любого случайного события AÎF имеет место равенство
то для любого случайного события AÎF имеет место равенство
P(A)= 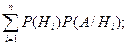 (6)
(6)
Равенство (4) называют формулой полной вероятности. Для доказательства заметим, что в силу (4)

В силу (5) случайные события Hi ÇA попарно несовместны. Поэтому

Формула (6) справедлива и для счетного набора событий, удовлетворяющего условиям (4) и (5).
Рассмотрим примеры применения формулы полной вероятности.
ЗАДАЧИ
1. Пусть имеется n одинаковых урн. Известно, что урна с номером i содержит mi белых шаров, всего же шаров в этой урне Ni. Наугад выбрана урна, а из нее шар. Какова вероятность того, что взят белый шар?
Пусть Hi — событие, состоящее в том, что выбрана урна с номером i, а А — событие, состоящее в том, что взят белый шар. Тогда


Следовательно, по формуле полной вероятности

2. Среди N экзаменационных билетов п «счастливых·». Студенты подходят за билетами один за другим. У кого больше вероятность взять «счастливый» билет: у того, кто подошел первым, или у того, кто подошел вторым?
Вероятность взять «счастливый» билет для первого студента равна, очевидно,  . Пусть А событие, состоящее в том, что второй студент взял «счастливый» билет. Можно сделать два предположения: H1 — первый студент взял «счастливый билет», H2 — первый не взял «счастливый» билет. По формуле полной вероятности
. Пусть А событие, состоящее в том, что второй студент взял «счастливый» билет. Можно сделать два предположения: H1 — первый студент взял «счастливый билет», H2 — первый не взял «счастливый» билет. По формуле полной вероятности

Итак, вероятность взять «счастливый» билет для второго студента также равна  .
.
Формулы Байеса.
Докажем следующую теорему.
Теорема. Пусть набор событий Hi ,i= 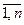 , образует полную группу событий, причем Р(Hi)>0 для каждого i=
, образует полную группу событий, причем Р(Hi)>0 для каждого i= 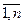 . Тогда для любого случайного события В такого, что Р(В)>0, выполнены равенства
. Тогда для любого случайного события В такого, что Р(В)>0, выполнены равенства
 (7)
(7)
Формулы (7) называются ф ο ρ м у л а м и Б а и е с а. Общая схема применения этих формул при решении практических задач следующая. Пусть событие B может происходить в различных условиях, о характере которых можно сделать п гипотез H1, H2....,Hn .
Из каких-то соображений известны вероятности этих гипотез Ρ (H1), ..., Ρ (Hn) (априорные вероятности), известны также условные вероятности Ρ (Β/ H1)..... Ρ (Β/Ηη). Предположим, что произведен опыт, в результате которого наступило событие B. Это должно вызвать переоценку вероятностей гипотез Hi; формулы Байеса и дают выражение для условных вероятностей P(Hi/B) (эти вероятности называются апостериорными вероятностями).
Для доказательства (7) используем формулу умножения и формулу полной вероятности. Имеем

Рассмотрим примеры применения формул Байеса.
ЗАДАЧИ
1. В урне находится п шаров. Возможна (п + 1) гипотеза о количестве белых шаров в урне: H0,H1,... Нп, (Hi —гипотеза, состоящая в том, что в урне i белых шаров. Предположим, что все эти гипотезы одинаково вероятны:

Из урны наугад взяли шар, который оказался белым. Пусть В — событие, состоящее в том, что наугад взятый шар из урны—белый. Вычислить Р(Hi/В).
Имеем Ρ (В/Hi) = 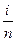 и по формуле (7)
и по формуле (7)

Таким образом, наиболее вероятной является гипотеза Нп.
2. Некоторая деталь производится на двух заводах. Известно, что объем продукции первого завода в n раз превышает объем продукции второго завода. Доля брака на первом заводе Р1, на втором Р2. Наугад взятая деталь оказалась бракованной. Какова вероятность того, что эта деталь выпущена первым заводом?
Пусть H1 — событие, состоящее в том, что взятая деталь изготовлена на первом заводе, H2 — событие, состоящее в том, что эта деталь изготовлена на втором заводе. Заметим, что

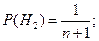
Пусть В — событие, состоящее в том, что наугад взятая деталь оказалась бракованной. По условию задачи Р(В/Н1) = Ρ1, (В/H2) = Р2. По формуле (7)
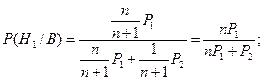
Дата добавления: 2016-02-27; просмотров: 2428;
