Барометрическая формула. Распределение Больцмана
При выводе уравнения (14) предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы газа находятся в поле тяготения Земли, поэтому их концентрация с высотой уменьшается. Покажем это.
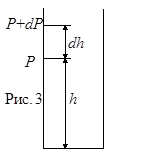
|
Рассмотрим газ в сосуде (см. рис. 3). Если атмосферное давление на высоте h равно Р, то на высоте h+dh оно равно Р+dP (при dh>0 dP<0, т.к. давление с высотой убывает). Разность давлений Р и Р+dP равна весу газа, заключенного в объеме цилиндра высотой dh с основанием 1 м2: Р -(Р+dP)=rgdh, где r - плотность газа. Следовательно,
dP= -rgdh. (19)
Воспользовавшись уравнением Клапейрона-Менделеева РV= 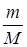 RT , находим, что
RT , находим, что 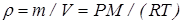 . Подставив это выражение в (19), получим
. Подставив это выражение в (19), получим
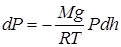 или
или 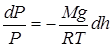 . (20)
. (20)
Интегрируя (20) от h=0 до h находим, 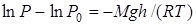 .Проведя потенцирование получим барометрическую формулу.
.Проведя потенцирование получим барометрическую формулу. 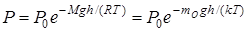 , (21)
, (21)
где m0=M/NA, k=R/NA.
Эта формула была впервые установлена в 1821 г. Лапласом.
Анализ барометрической формулы (21) показывает, что чем больше молярная масса М газа, тем быстрее его давление убывает с высотой. Поэтому атмосфера по мере увеличения высоты все более обогащается легкими газами.
Следует иметь в виду, что применимость формулы (21) к реальной атмосфере несколько ограничена, поскольку атмосфера в действительности не находится в тепловом равновесии, и ее температура меняется с высотой. Тем не менее, ее используют, определяя высоту по изменению давления.
Формулу (21) можно преобразовать, если воспользоваться выражением (9) Р=nkT
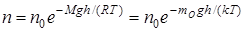 , (22)
, (22)
где m0gh=Wп - потенциальная энергия молекулы в поле тяготения, т.е.
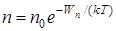 . (23)
. (23)
Больцман доказал, что формула (21) справедлива в случае потенциального поля любой природы (т.е. не только поля тяготения). В связи с этим функцию (23) называют распределением Больцмана.
Дата добавления: 2016-03-04; просмотров: 2012;
