Случайная величина полностью определяется своим распределением, функцией распределения или плотностью распределения

Лекция №5

Характеристики случайных величин

Характеристики положения

Математическое ожидание случайной величины

Определение. Если — дискретная случайная величина, принимающая значения x₁, х₂, ... с вероятностями р_1, р₂, ..., то ее математическим ожиданием называется величина

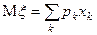(3)

при условии, что ряд справа абсолютно сходится.

2. Отметим следующую механическую интерпретацию математического
ожидания. Представим себе, что на числовой оси в точках с координатами
x₁, х₂, ..., х_п расположены массы р_1, р₂, , ...,_, р_n. Тогда

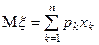
есть координата центра тяжести этой системы масс.

Свойстваматематического ожидания.

1) Если 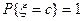, то .

2) Если — интегрируемая неотрицательная случайная вели­
чина, то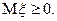

3) Если , то и .

4) Если — интегрируемая случайная величина, то a также интегрируема и

(10)

7) Если и интегрируемы, то сумма + также интегри­
руема и

. (11)

8) Если и — интегрируемые случайные величины, то при любых постоянных а и b случайная величина a +b также ин­тегрируема, причем

9) Если и — интегрируемые случайные величины и ,
то .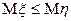

10) Если — неотрицательная величина и a > 0, то

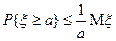
Это неравенство называется неравенством Чебышева.

Для доказательства рассмотрим величину , такую, что = 0 при <а и =а при 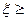а. Имеем 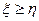и, следовательно, . Величина принимает два значения 0 и a, поэтому

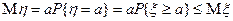
Медиана

Медианой 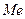- значение случайной величины, такое что

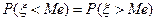
Если имеет место непрерывная случайная величина это равенство равносильно равенству площадей графика плотности распределения

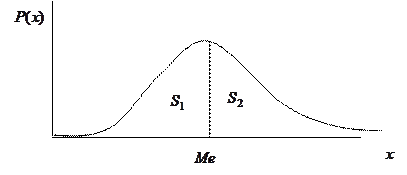Мода

Мода 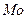характеризует наиболее вероятное значение случайной величины.