Аксиоматическое определение вероятности

До начала XX в. теория вероятностей представляла собой еще не сложившуюся науку, в которой основные понятия были недостаточно четко определены. Эта нечеткость приводила нередко к парадоксальным выводам (наиболее известные из них – парадоксы Бертрана). Возникающие противоречия подрывали имевшиеся представления о вероятности. Было объявлено, что понятие о вероятности пригодно только для конечного числа элементарных исходов (то, что сейчас называется элементарной теорией вероятностей), а для бесконечного числа исходов оно не пригодно. Однако такой подход не мог устраивать практиков, ведь на практике чаще приходилось сталкиваться именно с бесконечным числом исходов. К тому же, эти обстоятельства мало смущали естествоиспытателей, т.к. их наивный теоретико-вероятностный подход в различных областях науки приводил к крупным успехам (статистическая физика, квантовая механика и др.).

развитие естествознания в конце XIX – начале XX вв. предъявило к вопросам обоснования наук повышенные требования. Однако первые работы по аксиоматическому обоснованию теории вероятностей не дали удовлетворительного решения задачи. Наиболее перспективным оказался путь, предложенный французским математиком Э. Борелем, который подметил глубокую аналогию между вероятностью и мерой, одним из наиболее важных понятий современной теории функций. Определение вероятности как меры, позволило связать теорию вероятностей с метрической теорией функций и теорией множеств. На этой базе А.Н. Колмогорову (1933 г.) удалось построить логически совершенное здание современной теории вероятностей.

Отправным пунктом аксиоматики Колмогорова является пространство элементарных событий W, которое может быть множеством произвольной природы. Наряду с W рассматривается также система Á всех возможных событий (множество всех подмножеств). При этом множество Á должно быть булевой алгеброй, т.е. замкнуто относительно операций сложения и умножения событий, наряду с каждым событием А содержать противоположное событие , а также достоверное W и невозможное Æ события.

Если пространство W состоит из конечного числа N элементарных исходов, то общее число всех возможных событий, т.е. число элементов множества Á, равно 2^N. Действительно, Á содержит пустое подмножество Æ, C_N¹=N одноэлементных подмножеств, C_N² – двухэлементных подмножеств и т.д. В результате получаем, что всего событий будет .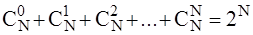

В тех случаях, когда W – бесконечное, дискретное или непрерывное, множество, попытка использовать в качестве системы Á все подмножества множества W наталкивается на серьезные трудности. Это связано с тем, что понятие множество всех подмножеств противоречиво. Поэтому для таких множеств W вводят ограничения на системы рассматриваемых подмножеств.

Система Á подмножеств W называется s-алгеброй (или борелевой алгеброй), если она является булевой алгеброй и, кроме того, замкнута относительно алгебраических операций над счетным числом событий, т.е. если A_n Î Á (n=1,2,3, ...), то

, .

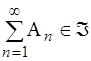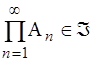Аксиоматическая теория Колмогорова основывается на четырех аксиомах, с помощью которых вводится понятие вероятности и некоторые ее свойства. Итак, каждому событию А из некоторой s-алгебры Á ставится в соответствие некоторое число P(A), которое называется вероятностью события А, и должна удовлетворять следующим аксиомам:

1⁰. Аксиома неотрицательности: P(A) £ 0.

2⁰. Аксиома нормированности: P(W) = 1.

3⁰. Аксиома сложения. Если события A₁, A₂,...,A_n попарно несовместны. то

P(A₁+A₂+...+A_n) = P(A₁)+P(A₂)+...+P(A_n).

4⁰. Расширенная аксиома сложения. Для любой бесконечной последовательности наблюдаемых попарно несовместных событий A₁, A₂,... справедливо равенство:

.

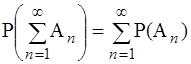Последняя аксиома нужна для создания полноценной математической теории, включающей и бесконечные множества. Однако приведенные свойства вероятности являются также и основными свойствами меры множества. Таким образом, теория вероятностей с формальной точки зрения можно рассматривать как часть теории меры.

Отметим, что приведенные аксиомы не содержат невозможного события Æ, поскольку из аксиом 1⁰-3⁰ следует, что вероятность события Æ равна нулю. Действительно, поскольку W+Æ=W и WÆ=Æ, то P(W) = P(W+Æ) = P(W)+P(Æ), откуда следует, что P(Æ)=0.

Тройка (W, Á,P), где W – пространство элементарных событий, Á – выделенная в W s-алгебра подмножеств, P – распределение вероятностей на Á, называется вероятностным пространством.

Система аксиом Колмогорова непротиворечива, т.к. существуют реальные объекты, которые всем этим аксиомам удовлетворяют. Однако эта система аксиом неполная, поскольку не содержит указаний о численных значениях вероятностей интересующих нас событий, а определяют лишь общие свойства, которыми должна обладать вероятность как числовая функция. Вопрос о том, какое значение вероятности следует приписать тому или иному событию в реальных экспериментах, решается методами математической статистики. Задача теории вероятностей состоит в вычислении сложных событий, зная вероятности элементарных событий.