Теоретико-множественная интерпретация событий
Как известно, для множеств определено отношение порядка и над ними можно производить определенные алгебраические операции. Проанализируем содержательное значение этих понятий в том случае, когда подмножества некоторого множества W интерпретируются как события, наблюдаемые о некотором эксперименте.
1. Само множество W, рассматриваемое как событие, характеризуется тем, что в результате эксперимента оно необходимо происходит. Действительно, никакие другие результаты эксперимента, крометех, которые описываются точками wÎW, по определению невозможны. Множество W. называют достоверным событием.
2. Подмножеством любого множества W считается пустое множествоÆ, не содержащее ни одной точки W. Если Æ отождествлять с событием, то это событие в эксперименте не происходит. Его называютневозможным событием.
3. Подмножества данного множества W частично упорядочены. Пишут  , если каждый элемент множества А содержится в В.
, если каждый элемент множества А содержится в В.
Если А и В — события, то  означает, что, если событие А происходит, то событие В также происходит. В этом случае говорят, что из события А следует событие В (событие А влечет за собой событие В). Очевидно, для любого А, А Ì W. По определению принимают
означает, что, если событие А происходит, то событие В также происходит. В этом случае говорят, что из события А следует событие В (событие А влечет за собой событие В). Очевидно, для любого А, А Ì W. По определению принимают
Æ Ì А
4.Суммой двух множеств А È В называют множество, содержащее все элементы, входящие или во множество А, или во множество В и не содержащее никаких других элементов.
Для событий это следует интерпретировать так: суммой (или объединением) двух событий А и В называют событие А È В, происходящее тогда и только тогда, когда происходит или событие А, или событие B.

Аналогичный смысл имеет сумма любого числа событий. Если I — произвольное множество значений некоторого индекса i, 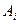 (i Î I) — некоторое множество событий, то
(i Î I) — некоторое множество событий, то
сумма.(объединение)  есть событие, происходящее тогда и только тогда, когда происходит
есть событие, происходящее тогда и только тогда, когда происходит
одно из событий 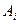 .
.
Заметим, что для любого A
A È Æ = A; А È W =W.
Событие А È В играет роль точной верхней грани событий А и В. Это надо понимать так:
А Ì А È В; В Ì А ÈВ,
и если событие С таково, что A Ì С и В Ì С, то А È В Ì С.
5. Операция пересечения двух (или любого числа) множеств определяется следующим образом: пересечение А Ç В (или Ç 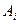 ) есть множество, состоящее из тех и только тех элементов,
) есть множество, состоящее из тех и только тех элементов,
iÎ I
которые принадлежат как множеству А, так и множеству В (всем множествам 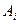 , iÎ I)
, iÎ I)
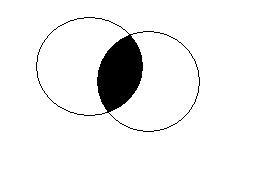
На языке алгебры событий событие АÇ В ( 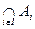 ) происходит тогда и только тогда, когда происходит и событие А, и событие В (все события
) происходит тогда и только тогда, когда происходит и событие А, и событие В (все события 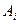 , i Î I).
, i Î I).
Пересечение событий называют также их совмещением. Отметим очевидные соотношения
A Ç Æ = Æ; A Ç W = A A Ç B Ì A; A Ç B Ì B
и если С Ì A Ç В, то С Ì A и С Ì В.
Таким образом, пересечение А Ì В можно рассматривать как точную нижнюю грань множеств A и В.
Отметим еще, что, как известно из теории множеств, в смысле введенного отношения порядка, операции Ç и È дистрибутивны:
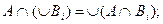
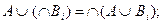
Условимся два события. A и В называть несовместимыми, или дизъюнктными, если их совмещение есть событие невозможное: A Ç B = Æ
Несовместимые события изображаются множествами, не имеющими общих точек,
Последовательность событий A1, A2, ... (конечная или бесконечная) называется дизъюнктной, или последовательностью несовместимых событий, если каждая пара из них является несовместимой:

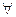 i, j; i¹ j.
i, j; i¹ j.
6. Каждому множеству A можно поставить в соответствие другое множество — его дополнение 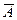 , состоящее из всех точек, которые не входят в A.
, состоящее из всех точек, которые не входят в A.
Таким образом,
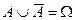 ,
, 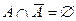 .
.
Если A—случайное событие, то 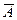 —событие происходящее тогда и только тогда, когда A не
—событие происходящее тогда и только тогда, когда A не
происходит. Событие 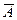 называют событием, противоположным A.
называют событием, противоположным A.
7. Разность A\В двух множеств A и В есть множество, состоящее из элементов, входящих в А, но не входящих в В. Если A и В — событие, то A\ В событие — происходящее тогда и только тогда, когда происходит A, но не происходит В.Очевидно  ,
, 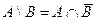
.

Подытоживая сказанное, приведем таблицу, показывающую, как некоторые понятия теории множеств интерпретируются в теории вероятностей.
| Обозначения | Язык теории множеств | Язык теории вероятностей |
| W | Универсальное множество | Пространство элементарных событий (элементарных исходов эксперимента) |
| w | Элемент W | Элементарное событие |
| А | Некоторое множество элементовw | Событие А (если wÎ А, то говорят что наступило событие А) |
| W | Множество всех w | Достоверное событие |
| Æ | Пустое множество | Невозможное событие |
| AÌB | А-подмножество B | Из наступления события А необходимо следует событие B |
| AÈB | 0бъединение множеств А и B; множество точек, входящих или в А или в B | Событие состоящее в том что произошло А или B |
| AÇB | Пересечение множеств А и В , множество точек входящих и в А и в B | Событие состоящее в том что произойдет и А и B |
| AÇB=Æ | А и B непересекающиеся множества | А и B несовместные события |
| A\B | Разность множеств А и B | Событие состоящее в том что произойдет А но не произойдет B |
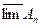
| Множество всех тех w которые принадлежат бесконечному числу множеств из последовательности { 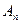 } }
| Событие состоящее в том что произойдет бесконечное число событий из последовательности { 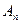 } }
|
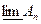
| Множество всех тех w которые принадлежат всем 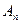 за исключением конечного числа (множество тех w которые не принадлежат только конечному числу множеств за исключением конечного числа (множество тех w которые не принадлежат только конечному числу множеств 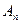 ) )
| Событие, состоящее в том, что произойдут все события 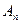 за исключением конечного числа, событие состоящее в том что не произойдет только конечное число из событий последовательности за исключением конечного числа, событие состоящее в том что не произойдет только конечное число из событий последовательности 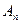
|
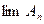
| Если  то последовательность множеств { то последовательность множеств { 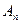 } имеет предел } имеет предел 
| Если 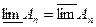 то последовательность событий { то последовательность событий { 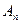 }Имеет предел }Имеет предел 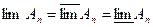
|
Лекция №3
Дата добавления: 2016-02-27; просмотров: 1741;
