Вероятностные модели экспериментов, аксиомы теории вероятностей, свойства вероятностей и событий.
Определение. Произвольное непустое множество 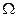 с произвольной сигма-алгеброй F подмножеств этого множества называется абстрактным пространством элементарных событий (исходов) с множеством (полем) F наблюдаемых событий абстрактного опыта. Будет использоваться обозначение
с произвольной сигма-алгеброй F подмножеств этого множества называется абстрактным пространством элементарных событий (исходов) с множеством (полем) F наблюдаемых событий абстрактного опыта. Будет использоваться обозначение 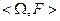 .
.
Вероятностной мерой (вероятностью) на пространстве абстрактного опыта 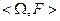 называется функция P, определённая на сигма-алгебре F, удовлетворяющая следующим условиям (свойствам, аксиомам).
называется функция P, определённая на сигма-алгебре F, удовлетворяющая следующим условиям (свойствам, аксиомам).
1) Аксиома неотрицательности. Каждому событию 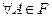 ставится в соответствии неотрицательное число P(A) называемое вероятностью события.
ставится в соответствии неотрицательное число P(A) называемое вероятностью события.
2) Аксиома нормированности. 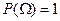
3) Аксиома сложения. Если 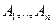 - это последовательность событий из F, таких, что они попарно несовместные, то вероятность сумм этих событий равняется сумме вероятностей.
- это последовательность событий из F, таких, что они попарно несовместные, то вероятность сумм этих событий равняется сумме вероятностей. 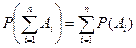
4) Расширенная аксиома сложения. Если 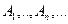 - это бесконечная последовательность событий из F, попарные – совместны, то вероятность сумму этих событий равняется сумме вероятностей событий.
- это бесконечная последовательность событий из F, попарные – совместны, то вероятность сумму этих событий равняется сумме вероятностей событий. 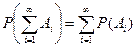
Определение 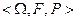 - тройка, состоящая из непустого множества, сигма-некоторая сигма-алгебра этого множества, вероятности события, называется (абстрактной) вероятностной моделью (абстрактного) опыта с распределением вероятностей на поле этого опыта.
- тройка, состоящая из непустого множества, сигма-некоторая сигма-алгебра этого множества, вероятности события, называется (абстрактной) вероятностной моделью (абстрактного) опыта с распределением вероятностей на поле этого опыта.
На данный момент можно дать следующее определение теории вероятностей. Предметом теории вероятностей является формальное изучение вероятностных моделей и взаимосвязанных с ними вопросов.
При построении вероятностной модели конкретного опыта, теория вероятности исходит из постулата, что с каждым опытом связана вероятностная модель этого опыта 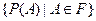 . При этом, постулируется в каждом опыте наличие множества элементарных исходов. И для решения большинства вопросов связанных с опытами, достаточно только предпологать наличие этих элементарных исходов, а не заниматься их детальным описанием.
. При этом, постулируется в каждом опыте наличие множества элементарных исходов. И для решения большинства вопросов связанных с опытами, достаточно только предпологать наличие этих элементарных исходов, а не заниматься их детальным описанием.
Относительно сигма-алгебры событий F предполагается, что все события, относительно которых рассматриваются какие-либо вопросы в опыте, они принадлежат некоторой сигма-алгебре. Например, пересечению всех сигма-алгебр событий, содержащих рассматриваемое событие. 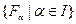 , то
, то 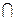
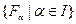 . То есть пересечение любого семейства сигма-алгебр, является сигма-алгеброй. Если рассматривать какое-либо семейство событий
. То есть пересечение любого семейства сигма-алгебр, является сигма-алгеброй. Если рассматривать какое-либо семейство событий 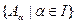 .
.
Правильность выбора функции P должна подстверждаться практикой применения абстрактной модели к конкретному опыту.
Рассмотрим простейшие формальные свойства вероятности событий.
1) 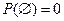 .
.
2) Если 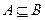 , то
, то 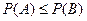 .
.
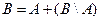
Доказательство:
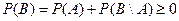
…
3) Теорема о согласованности со статистической вероятностью. 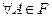
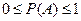 , то есть
, то есть 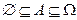 .
.
4) Теорема о вероятности противоположного события 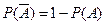
5) Теорема о вероятности объединения двух событий 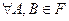 ,
, 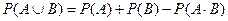 .
.
Доказательство:
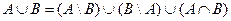
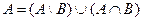
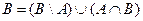
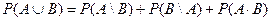
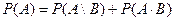
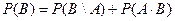
6) Теорема объединения вероятности n событий. 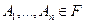
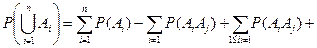
Дата добавления: 2016-04-11; просмотров: 1139;
