Конечным множеством.

Примеры

1. Предположим, монету бросают один раз. Пространство элементарных событий этого эксперимента имеет вид W = {Г, Р},где буква Г означает появление герба, буква Р — появление решки.

2. Монету бросают дважды. Пространством элементарных событий этого эксперимента является множество

W = {ГГ, ГР, РГ, РР}.

Здесь ГР означает, например, что при первом бросании появляется герб, а при втором — решка.

3. Бросают шестигранную игральную кость, на которой выбиты очки от 1 до 6. Нас интересует число выпавших очков.. Пространством элементар­ных событий здесь может быть множество, состоящее из чисел 1, 2, 3, 4, 5, 6.

4. Игральную кость бросают т раз. В качестве пространства элементар­ных событий можно рассматривать множество всех m-мерных векторов вида (I1,I2.....Im). где каждая компонента Ik принимает значения 1, 2, 3, 4, 5, 6.

Счетным множеством

Примеры

1. Предположим, что монету бросают до первого появления герба. Про­странством элементарных событий такого эксперимента является множество

W={w₁, w₂, .. , , w_n, ... ; w_¥ },

где (wn = Р...РГ означает, что герб впервые появится при n-м бросании

(n—1) раз

монеты, а w¥, соответствует той возможности, что герб никогда не появится (в этом случае наш эксперимент продолжается бесконечно долго).

Непрерывным множеством

Примеры

1. Стрелок стреляет по круглой мишени, и нас интересует точка, в кото­рую попала пуля. В качестве пространства элементарных событий можно принять множество, состоящее из рассматриваемого круга К и одной до­полнительной точки q, обозначающей непопадание стрелка в мишень.

2. Задача о встрече. Два лица А и В условились встретиться в интерва­ле времени [О, Т]. Если через х обозначим время прихода A, а через у время прихода В, то пространством элементарных событий будет множество

W = {(X ,У): 0<=X<=T, 0<=у<=T}.

3. Установлен автоматически работающий прибор, вычерчивающий график скорости ветра в данной точке атмосферы в течение данного интер­вала времени [T1, Т2]. Пространством элементарных событий может быть множество всех неотрицательных функций, заданных на интервале времени [T1 _г,T2 ] и имеющих, скажем, только конечное число разрывов первого рода.

4. Наблюдается частица, совершающая броуновское движение. Простран­ство элементарных событий — множество всех возможных траекторий частицы.

Случайные события

Случайные события — подмножества в пространстве элементар­ных событий. В теории вероятностей не рассматривается техниче­ская сторона эксперимента, а только то, какие события в нем могут наблюдаться и что в результате проведенного эксперимента дей­ствительно наблюдалось. Таким образом, с каждым экспериментом связывают некоторое множество событий, о которых можно судить, осуществилось ли оно в данном эксперименте или нет. Такие собы­тия называют наблюдаемыми в данном экспери­менте.

В эксперименте примера 3 нас интересует, превысила ли ско­рость ветра 10 м/с; это событие наблюдаемо. Если же по графику скорости ветра мы захотим судить, попал ли данный стрелок в ми­шень в примере 1, то сделать этого мы не сможем. Это событие не наблюдаемо в эксперименте примера 3

.

Пусть A — произвольное наблюдаемое в данном эксперименте событие. Поскольку каждое элементарное событие со дает полную информацию о результате эксперимента, то зная, что результат эксперимента описывается точкой w, всегда можно сказать, про­изошло A или нет. Таким образом, по отношению к событию A все пространство элементарных событий и можно разбить на два дополнительных множества А' и A" (A' Î W, А" Î W, А' È А" = W) так, что, если результат эксперимента описывается точкой w из множества А', то событие А в этом эксперименте произошло, если же w Î А", то событие А не произошло. Точки w из множества А' называют элементарными событиями, благоприятствующими со­бытию А.Говорят, что множество А' является отражением или интерпретацией события А во множестве W.

Следующий этап в построении теоретико-множественной модели теории вероятностей состоит в отождествлении события А и мно­жества А', А º А'.

Итак, в дальнейшем событие А — это некоторое подмножество W, состоящее, из всех тех точек w — элементарных событий,— ко­торые благоприятствуют событию А. Если результат эксперимента описывается точкой w и w входит в А, то в данном эксперименте событие А произошло, если же wÎ А, то событие А в этом экспе­рименте не произошло.

Примеры

1. Пусть монету бросают дважды и А —событие, состоящее в том, что хотя бы один раз появится герб. Тогда

W = {ГГ, ГР, РГ, РР}, А = {ГГ, ГР, РГ}.

2. Предположим, что один раз бросают игральный кубик и А — событие, состоящее в том, что число появившихся очков делится на 3. Тогда

W = {1. 2, 3, 4, 5, 6}; А = {3, 6}.

3. Предположим, что монету бросают до первого появления герба. Пусть А— событие, состоящее в том, что будет сделано не больше трех бросаний. Тогда

А = {Г, РГ, РРГ}.

4. Рассмотрим задачу о встрече Предположим, что каждое из лиц А и В ожидает другого время не больше чем t,0 < t < Т. Пусть С — событие, состоящее в том, что встреча произойдет. Тогда (рис. 1)

С - {(х, у):½х— у ½ < t, 0 < x < T, О <=у <= T}.

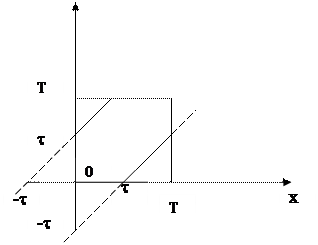
Рис.1