Свободные колебания упругих систем с конечным числом степеней свободы.
Свободные колебания возникают при начальных возмущениях системы. Если положение равновесия системы, принятое за начало координат, устойчиво, то при небольших начальных отклонениях от положения равновесия ( 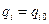 ,
, 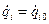 ) возникнут малые колебания, которые называются свободными. Для записи уравнений движения воспользуемся уравнениями Лагранжа:
) возникнут малые колебания, которые называются свободными. Для записи уравнений движения воспользуемся уравнениями Лагранжа:
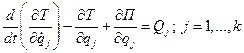 ;
;
где 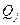 - обобщенные силы, не имеющие потенциал. В рассматриваемых ниже задачах обобщенные силы являются функциями времени, координат и скоростей точек системы
- обобщенные силы, не имеющие потенциал. В рассматриваемых ниже задачах обобщенные силы являются функциями времени, координат и скоростей точек системы 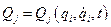 . Так как кинетическая энергия равна
. Так как кинетическая энергия равна 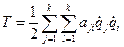 , то
, то
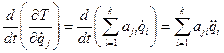 ,
, 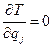 .
.
Тогда уравнения Лагранжа преобразуются к виду
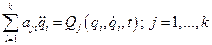 . (3.1)
. (3.1)
Это и есть уравнения колебательного движения. Механическая система консервативна, если для действующих на нее внешних и внутренних сил можно записать выражение потенциальной энергии. В этом случае уравнения движения удобно записать в матричной форме. Воспользуемся для этого полученным ранее выражением для потенциальной энергии
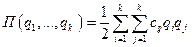 .
.
Вычислим обобщенную силу
 .
.
Уравнения движения (3.1) принимают вид
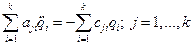
или в матричной форме
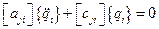 . (3.2)
. (3.2)
Здесь  - вектор (транспонированная матрица – столбец) обобщенных координат;
- вектор (транспонированная матрица – столбец) обобщенных координат; 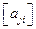 - квадратная матрица обобщенных коэффициентов инерции;
- квадратная матрица обобщенных коэффициентов инерции; 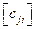 - квадратная матрица обобщенных коэффициентов жесткости. Решение уравнения (3.2) разыскивается в виде
- квадратная матрица обобщенных коэффициентов жесткости. Решение уравнения (3.2) разыскивается в виде
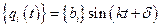 ,
,
где 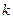 - частота колебаний;
- частота колебаний;  - матрица – столбец амплитуд. После подстановки предполагаемого вида решения в исходное матричное уравнение (3.2), получим
- матрица – столбец амплитуд. После подстановки предполагаемого вида решения в исходное матричное уравнение (3.2), получим

Это матричная запись однородной системы алгебраических уравнений. Она имеет нетривиальное решение, когда главный определитель матрицы равен нулю
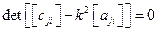 .
.
Корнями этого уравнения являются частоты свободных колебаний 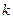 . Каждому значению частоты свободных колебаний соответствует собственный вектор
. Каждому значению частоты свободных колебаний соответствует собственный вектор  , который называют формой колебаний.
, который называют формой колебаний.
Если с помощью начальных условий в реальной системе задать соотношение амплитуд, соответствующих какой-то одной форме колебаний, то колебания будут происходить с соответствующей частотой 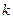 [8]. Если произвольно задать начальные условия, то колебания будут представлять смесь колебаний с различными частотами, то есть происходить в определенной пропорции.
[8]. Если произвольно задать начальные условия, то колебания будут представлять смесь колебаний с различными частотами, то есть происходить в определенной пропорции.
Применим основные теоретические положения, изложенные выше, для описания движения механической системы с двумя степенями свободы. Уравнение колебательного движения запишется в виде
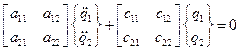 ; (3.3)
; (3.3)
Решение представляется в форме
 ;
; 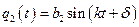 .
.
Или в матричной форме
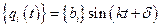 .
.
После подстановки предполагаемого решения в уравнение (3.3), имеем
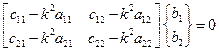 (3.4)
(3.4)
Это матричная запись системы однородных алгебраических уравнений. Ее нетривиальное решение возможно только в случае равенства нулю ее определителя:
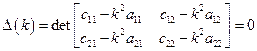 .
.
Частоты свободных колебаний определяются из уравнения
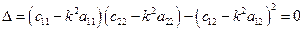
или в развернутой форме
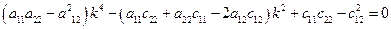 (3.5)
(3.5)
При раскрытии определителя учтено, что 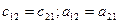 .
.
Выражение (3.5) называется частотным уравнением. Корни 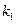 и
и 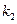 этого уравнения должны быть вещественными и положительными, так как колебания совершаются около устойчивого положения равновесия. Частоты
этого уравнения должны быть вещественными и положительными, так как колебания совершаются около устойчивого положения равновесия. Частоты 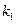 и
и 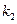 называются собственными или главными. Они не зависят от обобщенных координат и начальных условий, а определяются только инерционно–жесткостными характеристиками самой колебательной системы.
называются собственными или главными. Они не зависят от обобщенных координат и начальных условий, а определяются только инерционно–жесткостными характеристиками самой колебательной системы.
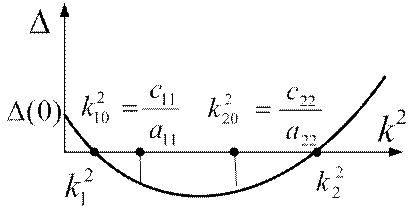
Рис.3.1
Если коэффициенты 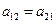 и
и 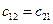 равны нулю, то система дифференциальных уравнений распадается на два независимых уравнения
равны нулю, то система дифференциальных уравнений распадается на два независимых уравнения
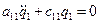 ;
; 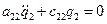 ,
,
в которых 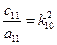 ,
, 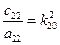 представляют собой частоты парциальных колебаний. В этом случае колебания по каждой обобщенной координате происходят независимо.
представляют собой частоты парциальных колебаний. В этом случае колебания по каждой обобщенной координате происходят независимо.
Подставляя поочередно найденные частоты 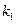 и
и 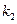 в систему (3.4), находим отношения амплитуд:
в систему (3.4), находим отношения амплитуд:
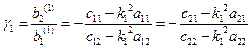 ;
; 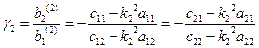 .
.
Величины 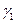 и
и  определяются только инерционно–жесткостными характеристиками системы и не зависят от начальных условий. Они называются коэффициентами распределения амплитуд по частотам. Формы колебаний – это набор амплитудных значений обобщенных координат:
определяются только инерционно–жесткостными характеристиками системы и не зависят от начальных условий. Они называются коэффициентами распределения амплитуд по частотам. Формы колебаний – это набор амплитудных значений обобщенных координат: 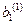 ;
;  - первая форма колебаний;
- первая форма колебаний; 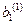 ;
;  - вторая форма колебаний. То есть для каждой собственной частоты существует своя форма колебаний.
- вторая форма колебаний. То есть для каждой собственной частоты существует своя форма колебаний.
Частные решения системы уравнений (главные колебания) для частот 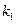 и
и 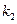 запишутся так:
запишутся так:
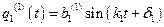 ;
; 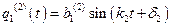 ;
;
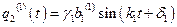 ;
; 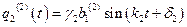 .
.
В силу линейности системы уравнений (3.4) общее решение запишется как сумма главных колебаний по каждой координате
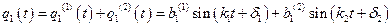 ; (3.6)
; (3.6)
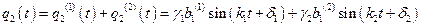 . (3.7)
. (3.7)
Четыре произвольные постоянные, содержащиеся в (3.8) и (3.9) находятся из начальных условий: 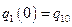 ,
, 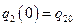 ,
, 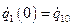 ,
,  . Таким образом, колебания по каждой координате есть наложение двух главных колебаний. Общий колебательный процесс не будет периодическим, если частоты
. Таким образом, колебания по каждой координате есть наложение двух главных колебаний. Общий колебательный процесс не будет периодическим, если частоты 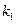 и
и 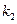 существенно отличаются.
существенно отличаются.
Формы колебаний определяются с точностью до постоянного множителя, поэтому обычно их нормируют. Один из способов нормирования: принять 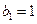 , тогда
, тогда
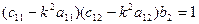 ;
;  .
.
При такой нормировке коэффициенты 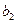 называют коэффициентами формы. Если форма колебаний такова, что
называют коэффициентами формы. Если форма колебаний такова, что 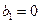 и
и  , то такая нормировка не годится.
, то такая нормировка не годится.
ПРИМЕР 1. Определить частоты и формы свободных колебаний системы, считая известными жесткость  пружин и массу
пружин и массу 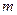 материальных точек.
материальных точек.

Рис. 3.2
РЕШЕНИЕ. Введем обобщенные координаты: 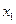 и
и 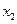 , которые определяют абсолютные смещения масс относительно положения равновесия. Кинетическая и потенциальная энергии вычисляются по формулам
, которые определяют абсолютные смещения масс относительно положения равновесия. Кинетическая и потенциальная энергии вычисляются по формулам
 ;
; 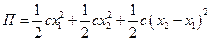 .
.
Найдем обобщенные коэффициенты инерции и жесткости:
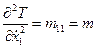 ,
,  ,
, 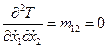 ,
,

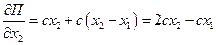
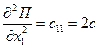 ,
, 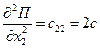 ,
, 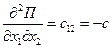 .
.
Составляем матрицы инерции и жесткости
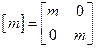 ;
; 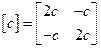 .
.
Частотное уравнение 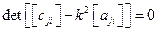 принимает вид
принимает вид
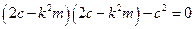 .
.
Ряд несложных преобразований
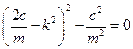 ;
; 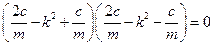 ;
; 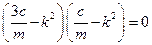 ;
;
позволяет найти корни уравнения
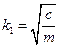 ,
,  .
.
Для определения форм собственных колебаний воспользуемся уравнением
 ,
,
матричная форма которого для рассматриваемого примера записывается в виде
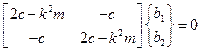 . (3.8)
. (3.8)
Подставим первый корень 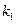 в это матричное уравнение
в это матричное уравнение
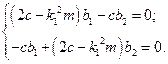 (3.9)
(3.9)
Система (3.9) состоит из двух линейно-зависимых уравнений, поэтому форму колебаний можно найти только с точностью до постоянного множителя. Нормируя форму 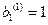 , из первого уравнения системы (3.9), находим
, из первого уравнения системы (3.9), находим
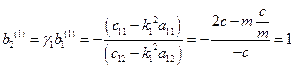 .
.
Повторяя эту процедуру для второго корня 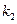 , находим нормированную форму колебаний
, находим нормированную форму колебаний
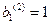 ,
, 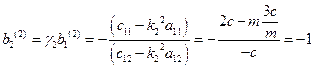 ,
,
которая соответствует второй собственной частоте. Графическое изображение первой и второй форм колебаний представлено на рис. 3.3.

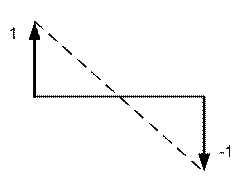
Рис. 3.3
Законы изменения обобщенных координат являются суммами главных колебаний
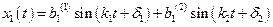 ;
;
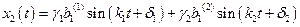 .
.
ПРИМЕР 2. Определить частоты и формы свободных колебаний системы (рис.3.4), считая известными жесткость пружины  , а также массы и геометрические размеры твердых тел, входящих в состав плоского механизма.
, а также массы и геометрические размеры твердых тел, входящих в состав плоского механизма.
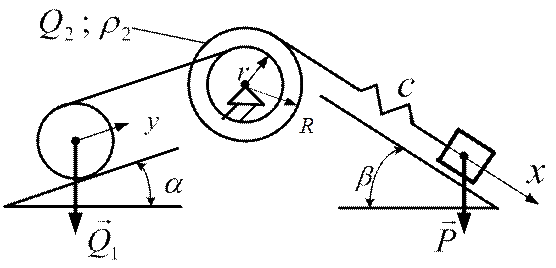
Рис.3.4
РЕШЕНИЕ. Это система с двумя степенями свободы. В качестве обобщенных координат выбираем перемещения груза 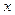 и центра диска
и центра диска 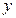 . Кинетическая энергия механизма записывается в форме
. Кинетическая энергия механизма записывается в форме
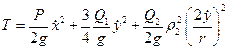 .
.
Вычисляем обобщенные коэффициенты инерции для частного случая, когда 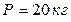 ,
, 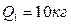 ,
,  ,
, 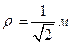 ,
, 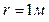
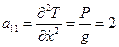 ;
; 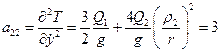 ;
; 
Запишем потенциальную энергию системы
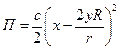 . (3.10)
. (3.10)
Заметим, что потенциальная энергия поля тяготения не содержит слагаемых, зависящих от 2-ой степени обобщенных координат, поэтому она не учитывается в выражении (3.10). Вычисляем величины обобщенных жесткостей, полагая 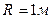 и
и 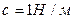
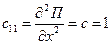 ;
; 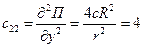 ;
;  .
.
Уравнение движения записывается в матричной форме:
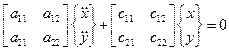 ;
; 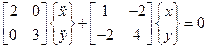 . (3.11)
. (3.11)
Решение этого матричного дифференциального уравнения будем разыскивать в форме
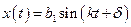 ;
; 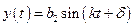 .
.
После подстановки решения в уравнение (3.11), приходим к однородному алгебраическому матричному уравнению
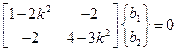 . (3.12)
. (3.12)
Для отыскания нетривиального решения, приравняем определитель матрицы уравнения к нулю, в результате приходим к частотному уравнению
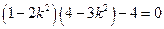 .
.
Его корни (собственные частоты) равны
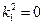 ;
; 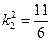 .
.
Коэффициенты распределения амплитуд 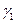 и
и  определяем из уравнения (3.12) в результате последовательной подстановки в него собственных частот
определяем из уравнения (3.12) в результате последовательной подстановки в него собственных частот 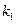 и
и 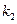 :
:
для частоты 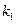 находим
находим 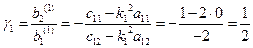 ;
;
для частоты 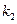 находим
находим 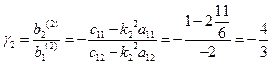 .
.
Теперь можно записать выражения для нормированных форм колебаний (рис.3.5):
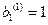 ,
, 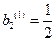 - первая форма;
- первая форма;
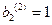 ,
,  - вторая форма.
- вторая форма.

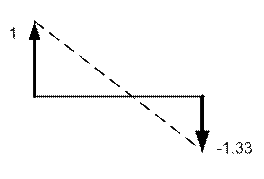
Рис.3.5
Законы изменения обобщенных координат записываются как линейные комбинации главных колебаний:
 ;
;
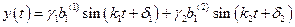 .
.
ПРИМЕР 3. Для двойного математического маятника, изображенного на рисунке 3.6, получить линейную модель и найти частоты и формы ее главных колебаний.
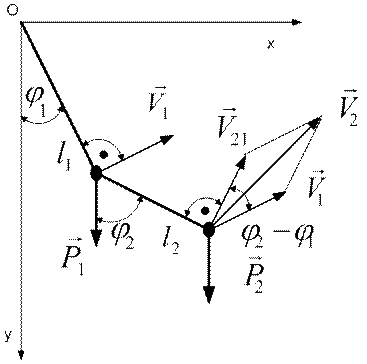
Рис.3.6
РЕШЕНИЕ. Для получения дифференциальных уравнений движения воспользуемся уравнениями Лагранжа второго рода для консервативных механических систем:
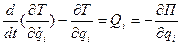 ;
; 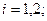 где
где 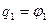 ;
; 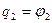 .
.
Составим выражение для кинетической энергии двойного математического маятника:
 .
.
Скорость второй тяжелой точки представляется как сумма 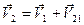 , где
, где 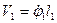 - скорость переносного движения с первой тяжелой точкой, а
- скорость переносного движения с первой тяжелой точкой, а 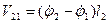 - относительного вращения вокруг первой точки. Тогда
- относительного вращения вокруг первой точки. Тогда
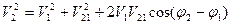 .
.
Выбрав в качестве независимых обобщенных координат углы с вертикалью 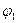 и
и 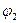 , выражение для кинетической энергии можно привести к виду:
, выражение для кинетической энергии можно привести к виду:
 .
.
Составим выражение для потенциальной энергии и найдем обобщенные силы, соответствующие обобщенным координатам 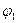 и
и 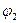 . Для этого вычислим работу сил
. Для этого вычислим работу сил  и
и 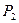 при перемещении системы из отклоненного положения в горизонтальное (принятое за положение с нулевой потенциальной энергией):
при перемещении системы из отклоненного положения в горизонтальное (принятое за положение с нулевой потенциальной энергией):
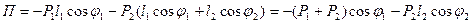 .
.
Выполнив дифференцирование, получим формулы для обобщенных сил:
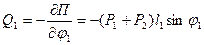 и
и 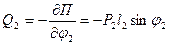 .
.
Для анализа малых колебаний целесообразно представить потенциальную и кинетическую энергии в виде разложений в степенные ряды Маклорена, т.е. для малых отклонений от положения равновесия справедливы приближенные равенства: 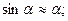
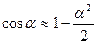 . В результате приходим к приближенным формулам для вычисления кинетической и потенциальной энергий
. В результате приходим к приближенным формулам для вычисления кинетической и потенциальной энергий
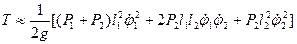 ;
;
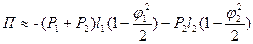 .
.
Перейдем к вычислению слагаемых, входящих в уравнения Лагранжа второго рода:
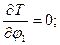
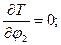
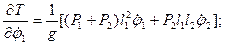
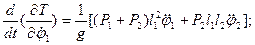
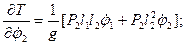
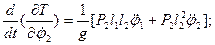
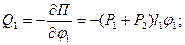
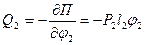 .
.
Составим уравнения Лагранжа в линеаризованной форме:
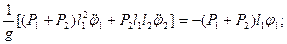
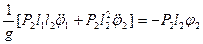 .
.
Приведем полученную систему линейных дифференциальных уравнений к стандартному виду:
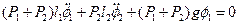 ;
;
 .
.
Тогда уравнение частот примет вид
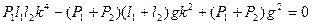 .
.
Для окончательного решения целесообразно задать числовые значения соответствующих величин либо достаточно простые соотношения между ними. Так, для частного случая 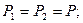
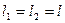 , уравнение примет вид
, уравнение примет вид
 .
.
Из него достаточно просто найти частоты главных колебаний
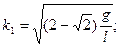
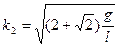 .
.
Коэффициенты распределения амплитуд 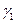 и
и  определяем из уравнения (3.12) в результате последовательной подстановки в него собственных частот
определяем из уравнения (3.12) в результате последовательной подстановки в него собственных частот 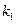 и
и 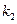 :
:
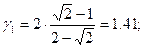
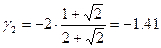 .
.
Дата добавления: 2016-02-11; просмотров: 3353;
