Динамический гаситель колебаний.

В качестве примера рассмотрим работу динамического гасителя колебаний. На рис.3.12.а схематично изображен механизм массой 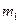, установленный на упругих опорах суммарной жесткостью в вертикальном направлении .

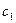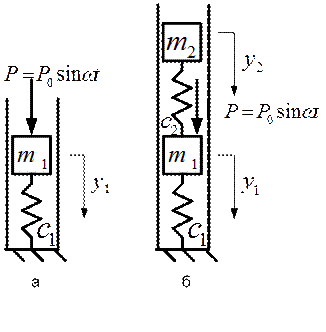
Рис.3.12

Если частота 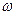возмущающей силы 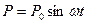, создаваемой движущимися внутри механизма неуравновешенными частями, совпадает с частотой 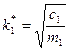свободных колебаний механизма на опорах, будет иметь место резонанс. Что бы этого избежать, установим на механизме массу 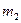на пружине жесткостью 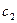. Новая механическая система, обладающая двумя степенями свободы, изображена на рис.3.12.б.

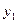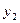Выберем в качестве обобщенных координат и , которые представляют собой абсолютные смещения по вертикали соответствующих масс от их положений статического равновесия. Мысленно отделим массы 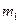и 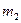, приложим к ним действующие силы; запишем для каждой из масс дифференциальное уравнение вертикального движения:

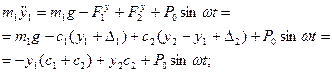
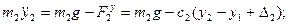
где 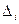- удлинение 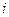- ой пружины в положении статического равновесия. Приведем уравнения системы к виду (3.18)

;

.

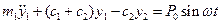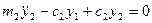Будем искать частное решение в виде

.

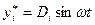Выполнив ряд действий, обсужденных выше, получим систему линейных алгебраических уравнений относительно 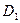и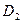

;

.

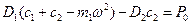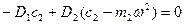Решение системы будет иметь вид:

.

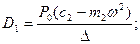
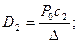
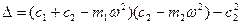Потребуем, чтобы амплитуда вынужденных колебаний механизма 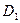была бы равна нулю, тогда массу 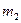и жесткость 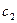присоединяемого элемента следует подобрать так, чтобы 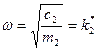. В этом случае присоединяемый элемент оказывается для основного механизма динамическим гасителем колебаний. Собственные частоты основного механизма 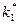и присоединяемого элемента 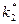называются их парциальными частотами.

Вид зависимостей для амплитуд колебани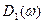й и 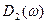приведен на рисунке 3.13.

Рис.3.13

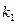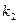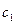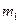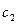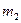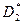На рисунке указаны следующие величины: и - собственные частоты механической системы, состоящей из основного механизма ( и ) и присоединяемого элемента ( и ); - амплитуда вибрации присоединяемого элемента при частоте вынуждающего воздействия, совпадающей с парциальной частотой основного механизма (а так же равной ей парциальной частоте присоединенного элемента).

Очевидно, что при 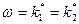должно выполняться соотношение

.

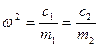Анализ этого соотношения показывает, что при сравнительно малой массе гасителя ( 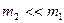) его жесткость 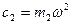так же должна быть сравнительно малой. Отмеченная особенность приводит к значительной амплитуде колебаний 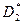гасителя, что опасно либо технически нереализуемо.

В реальной механической системе всегда имеют место силы сопротивления, приводящие к невозможности полного гашения колебаний основного механизма. Более подробно с влиянием этого фактора можно ознакомиться в [8].