Кинетическая энергия консервативных механических систем.
Рассмотрим несвободную систему с 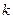 степенями свободы, на которую наложены идеальные голономные связи. Декартовы координаты
степенями свободы, на которую наложены идеальные голономные связи. Декартовы координаты 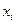 ,
, 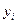 и
и 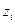 , определяющие положения материальных точек системы, связаны с обобщенными координатами
, определяющие положения материальных точек системы, связаны с обобщенными координатами 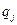 соотношениями
соотношениями
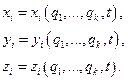
В векторной форме эти уравнения записываются в виде 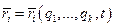 , где
, где 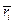 - позиционные радиусы-векторы системы. Скорость
- позиционные радиусы-векторы системы. Скорость 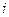 -ой точки системы равна
-ой точки системы равна
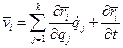 .
.
Кинетическая энергия механической системы вычисляется по формуле
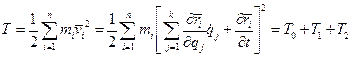
Здесь 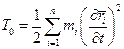 ;
; 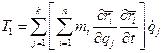 ;
; 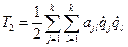 ,
,
Коэффициенты 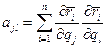 являются функциями координат
являются функциями координат 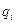 и времени
и времени 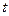 , потому что зависят от радиусов-векторов
, потому что зависят от радиусов-векторов 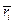 .
.
В случае стационарных связей 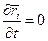 . Следовательно
. Следовательно 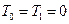 , коэффициенты
, коэффициенты 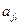 не зависят от времени и являются функциями только координат
не зависят от времени и являются функциями только координат 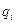 . Кинетическая энергия может быть записана как однородная определенно положительная квадратичная форма обобщенных скоростей
. Кинетическая энергия может быть записана как однородная определенно положительная квадратичная форма обобщенных скоростей
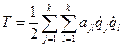 .
.
Если колебания системы малые, то коэффициенты 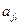 можно разложить в ряд по степеням
можно разложить в ряд по степеням 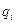 в положении равновесия, ограничившись членами первого порядка малости, т.е.
в положении равновесия, ограничившись членами первого порядка малости, т.е.
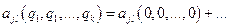 .
.
Величины 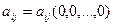 принято называть коэффициентами инерции. Заметим, что
принято называть коэффициентами инерции. Заметим, что 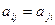 .
.
Дата добавления: 2016-02-11; просмотров: 729;
