Внутренняя энергия газа

Внутренней энергией газа называется сумма потенциальной и кинетической энергии всех его молекул:

.

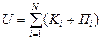Для большинства газов при условиях, близких к нормальным, потенциальной энергией взаимодействия молекул можно пренебречь. Пусть <e> – средняя кинетическая энергия молекулы газа. Тогда

U = N<e>,

где N – число молекул.

Если газ одноатомный, то

.

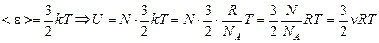Таким образом,

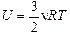. (19.1)

Поскольку согласно уравнению Менделеева–Клайперона pV = =nRT, то справедливо также

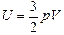. (19.2)

Если газ двухатомный, то необходимо учитывать кинетическую энергию вращательного движения молекул, поэтому

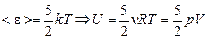. (19.3)

Задача 19.1. Найти изменение внутренней энергии 1 г Не и 1 г О₂ при нагревании их на 1 К.

т = 1 г Не: m1 = 4 г/моль О2: m2 = 32 г/моль DТ = 1 К	Решение. Заметим, что гелий (Не) – одноатомный газ, а кислород (О2) – двухатомный. Тогда
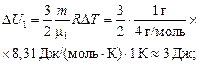
DU1 = ? DU2 = ?

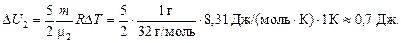
Ответ: DU₁ » 3 Дж; DU₂ » 0,7 Дж.

Получилось, что 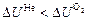. Это так, потому что в 1 г молекул Не больше, чем 1 г молекул О₂.

СТОП! Решите самостоятельно: А1, А2, А4–А6.

Задача 19.2. В комнате объема V = 100 м³ при атмосферном давлении р = 100 кПа находится воздух. Считая все молекулы воздуха двухатомными, найти внутреннюю энергию воздуха.

V = 100 м3 р = 100 кПа	Решение. Согласно формуле (19.3) 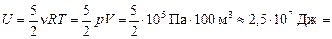= 25 МДж.
U = ?

Ответ: U = 25 МДж.

СТОП! Решите самостоятельно: В3–В6.

Задача 19.3. Воздух в комнате объема V = 100 м³ находится при температуре Т = 300 К и давлении р = 1,0×10⁵ Па. На сколько повысится внутренняя энергия воздуха при повышении температуры на DТ = 1 К? (Все молекулы считать двухатомными.)

V = 100 м3 Т = 300 К р = 1,0×105 Па DТ = 1 К	Решение. Согласно формуле (19.3) 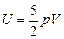. Так как р = const и V = const, то и U = const. Значит, DU = 0. Ответ: DU = 0.
DU = ?

Дело в том, что повысилась средняя кинетическая энергия молекул, но при этом часть молекул покинула комнату из-за расширения воздуха при нагревании.

Задача 19.4. В первом сосуде находятся N₁ = 1,00×10²⁰ молекул водорода при Т₁ = 300 К, во втором сосуде N₂ = 2,00×10²⁰ молекул кислорода при Т ₂ = 400 К. Сосуды соединили. Найти температуру и внутреннюю энергию смеси.

N1 = 1,00×1020 N2 = 2,00×1020 Т1 = 300 К Т 2 = 400 К	Решение. С одной стороны: 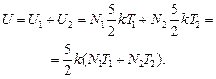С другой стороны:
Т = ? U = ?

.

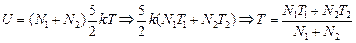Подставим численные значения:

.

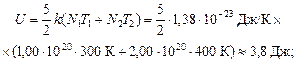
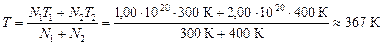Ответ: U » 3,8 Дж; Т » 367 К.

СТОП! Решите самостоятельно: С3, D2.

Задача 19.5. В горизонтальном цилиндре под поршнем находится одноатомный газ при атмосферном давлении р₀. Объем газа V₀. Поршень, площадь которого S, прикреплен ко дну цилиндра пружиной жесткости k, которая в начальный момент не растянута (рис. 19.1). Какое количество теплоты надо медленно подвести к газу, чтобы поршень сместился вправо на расстояние h?

V0 р0 k h S	Решение. Воспользуемся первым началом термодинамики: Q = A + DU. (1) Найдем А. Сила, с которой газ давит на поршень, должна равняться сумме сил давления атмосферы и упругости пружины:	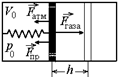Рис. 19.1
Q = ?

F_газа = F_атм + F_пр.

Тогда работа газа по модулю будет равна сумме абсолютных значений работ атмосферного воздуха и пружины:

|A_газа| = |A_пр| + |А_{атм.воз}|,

где 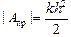, |А_{атм.воз}| = р₀Sh. Отсюда

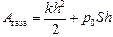. (2)

Найдем DU = U₁ – U₀. Воспользуемся формулой для внутренней энергии одноатомного газа: 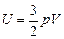, тогда

, ,

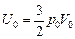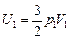где 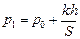, V₁ = V₀ + Sh. Отсюда

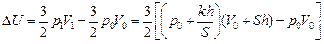. (3)

Подставляя (2) и (3) в (1), получим ответ:

Q = A + DU = + .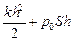

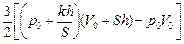СТОП! Решите самостоятельно: С4, С7, D4.