УРАВНЕНИЯ СОСТОЯНИЯ ГАЗА
Задача 20.1. Молекула массой т подлетает со скоростью υ перпендикулярно к стенке и испытывает абсолютно упругий удар. Длительность удара t. Найти среднюю силу давления молекулы на стенку.
| т υ t | Решение. Согласно закону изменения импульса
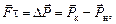 где
где  , ,  . Отсюда . Отсюда
| |
| F = ? | ||
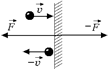 Рис. 20.1
Рис. 20.1
| 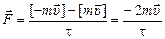 . .
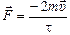 – это сила, с которой стенка действует на молекулу. – это сила, с которой стенка действует на молекулу.
| |
По третьему закону Ньютона молекула действует на стенку с такой же по величине, но противоположной по направлению силой
 .
.
Итак, сила, с которой молекула действует на стенку, по величине равна
 . (20.1)
. (20.1)
Задача 20.2. Молекула массой т подлетает со скоростью υ под углом a к стенке и испытывает абсолютно упругий удар. Длительность удара t (рис. 20.2,а). Найти среднюю силу давления молекулы на стенку.
а 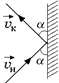 б б  Рис. 20.2
Рис. 20.2
| |
| т υ a t | |
| F = ? | |
Решение. 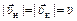 . Как видно из рис. 20.2,б,
. Как видно из рис. 20.2,б,

Тогда 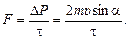
Ответ:
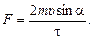 (20.2)
(20.2)
Задача 20.3. В течение времени t о стенку упруго ударяются n молекул. Скорости молекул υ и направлены перпендикулярно стенке (рис. 20.3). Найти среднюю силу, с которой молекулы действуют на стенку.
| υ t n | Решение. Каждая молекула передает стенке импульс DР1 = 2тυ, следовательно, n молекул передают стенке импульс
DР = 2тυn,
тогда 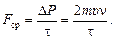 Ответ:
Ответ:
|  Рис. 20.3
Рис. 20.3
|
| Fср = ? | ||
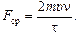 (20.3)
(20.3)
Задача 20.4. Пучок молекул, летящих в одном направлении со скоростью υ, попадает в стенку, расположенную перпендикулярно их движению. Сколько молекул ударится о стенку за время t? Площадь сечения пучка S, концентрация (число молекул в единице объема) п. Удары считать абсолютно неупругими.
| п υ S t | Решение. За время t о стенку ударятся только те молекулы, которые находятся от нее не дальше, чем l = υt (остальные не успеют долететь). Эти молекулы как бы образуют цилиндр площадью основания S и высотой l (рис. 20.4). Объем этого цилиндра |
| n = ? | |
 V = Sl = Sυt.
V = Sl = Sυt.
Число молекул в данном объеме
n = пV = пSυt.
Ответ:
n = пSυt. (20.4)
Задача 20.5. В сосуде, имеющем форму прямоугольного параллелепипеда, содержится газ. Концентрация молекул п, их средняя скорость υ. Определить число ударов за время t об основание сосуда площадью S.
| п υ S t | Решение. Сделаем упрощающее предположение: будем считать, что все молекулы движутся только в трех взаимно перпендикулярных направлениях: вдоль осей х, у и z (как по, так и против направления этих осей) (рис. 20.5). Таким образом, о нижнее основание параллелепипеда S могут ударяться молекулы, летящие только |
| n = ? | |
 вдоль оси z, причем те, у которых
вдоль оси z, причем те, у которых 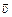 направлена вниз. Если в сосуде N молекул, то молекул, летящих вертикально вниз, N/6. (Молекулы в силу хаотичности своего движения делятся на 6 одинаковых по численности групп: 1) по оси х; 2) против оси х; 3) по оси у; 4) против оси у; 5) по оси z; 6) против оси z.) Следовательно, концентрация молекул, имеющих направление вертикально вниз, равна п1 = п/6.
направлена вниз. Если в сосуде N молекул, то молекул, летящих вертикально вниз, N/6. (Молекулы в силу хаотичности своего движения делятся на 6 одинаковых по численности групп: 1) по оси х; 2) против оси х; 3) по оси у; 4) против оси у; 5) по оси z; 6) против оси z.) Следовательно, концентрация молекул, имеющих направление вертикально вниз, равна п1 = п/6.
Тогда согласно формуле (20.4)
n = п1Sυt = 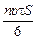 .
.
Ответ:
 (20.5)
(20.5)
Задача 20.6. Оценить давление газа на стенки сосуда. Считать, что скорость каждой молекулы υ, масса т, концентрация молекул п.
| п υ т | Решение. Из опыта известно, что давление не зависит от формы сосуда, поэтому расчет будем проводить для сосуда, имеющего форму прямоугольного параллелепипеда. Сделаем предположение, что молекулы движутся только в трех взаимно перпендикулярных направлениях, |
| р = ? | |
совпадающих с ребрами параллелепипеда. Удары о стенки молекул будем считать абсолютно упругими. Тогда
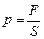 .
.
Согласно (20.3)  где n – число ударов за время t. Согласно (20.5)
где n – число ударов за время t. Согласно (20.5) 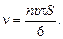 Тогда
Тогда
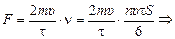
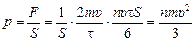 .
.
Ответ:
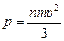 . (20.6)
. (20.6)
Наш расчет носит достаточно грубый, оценочный характер. Однако величина давления р, полученная при строгом расчете, оказывается точно такой же: 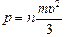 , только здесь υ2 – средний квадрат скорости молекул, т.е.
, только здесь υ2 – средний квадрат скорости молекул, т.е.
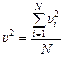 ,
,
где υi – скорость i-й молекулы; N – число молекул.
Почему же наши приближенные вычисления привели к верному результату?
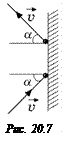 1. Удары молекул о стенку, вообще говоря, неупругие, но так как в среднем скорость молекул не меняется, то на всякую молекулу, подлетающую к стенке со скоростью υ, можно найти молекулу, в тот же момент отлетающую от стенки и с такой же скоростью υ, причем такую, что угол подлета первой молекулы равен углу отлета второй молекулы (рис. 20.7). Поэтому для огромного числа молекул предположение об упругом соударении справедливо.
1. Удары молекул о стенку, вообще говоря, неупругие, но так как в среднем скорость молекул не меняется, то на всякую молекулу, подлетающую к стенке со скоростью υ, можно найти молекулу, в тот же момент отлетающую от стенки и с такой же скоростью υ, причем такую, что угол подлета первой молекулы равен углу отлета второй молекулы (рис. 20.7). Поэтому для огромного числа молекул предположение об упругом соударении справедливо.
2. Мы не учли столкновений молекул. Но соударения не влияют ни на среднюю скорость, ни на число молекул, летящих в данном направлении в силу хаотичности столкновений и большого числа молекул.
3. Мы предположили, что молекулы летят в трех взаимно перпендикулярных направлениях. Из-за этого мы занизили число ударов о стенку. Согласно точному расчету 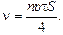
4. Мы завысили импульс, передаваемый молекулой стенке: 2тυ, а на самом деле 2тυsina. Поэтому усредненное по углам значение импульса меньше, чем 2тυ.
В итоге упрощающие предположения 3 и 4 скомпенсировали друг друга! Итак:
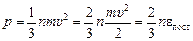
или
 , (20.7)
, (20.7)
где пeпост – суммарная энергия поступательного движения п молекул; eпост – средняя энергия поступательного движения одной молекулы.
Заметим, что уравнение  , где υ2 – средний квадрат скорости молекул, называется основным уравнением молекулярно-кинетической теории.
, где υ2 – средний квадрат скорости молекул, называется основным уравнением молекулярно-кинетической теории.
Таким образом, давление численно равно двум третям энергии поступательного движения молекул, содержащихся в единице объема.
Заметим, что двухатомная, а уж тем более трехатомная молекула не только движется поступательно, но еще и вращается в разных плоскостях. Кроме того, их атомы могут совершать колебания относительно центра молекулы. Эти движения не оказывают влияния на величину давления газа на стенку. А для одноатомных молекул они вообще невозможны.
СТОП! Решите самостоятельно: С1–С3, С6.
Дата добавления: 2016-04-11; просмотров: 1036;
