Что же такое – температура?
Сравним выражения
р =nkT и 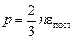 .
.
Приравняв правые части равенств, получим
nkT  Þ
Þ
 . (20.8)
. (20.8)
(Уже знакомая нам формула, которую раньше мы принимали на веру!) Отсюда
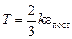 .
.
Таким образом: абсолютная температура есть величина, пропорциональная средней энергии поступательного движения молекул.
Заметим, что средняя энергия молекул зависит только от температуры и не зависит от массы молекул.
Из формулы (20.8) легко выразить среднюю квадратичную скорость через температуру:
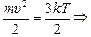
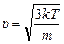 . (20.9)
. (20.9)
Задача 20.7. Сосуд, в котором находится газ молярной массы m при температуре Т, ускорили толчком до скорости и. Изменилась ли при этом температура газа? Изменится ли температура газа, если сосуд потом остановить?
| m Т и |  Рис. 20.8
Рис. 20.8
| Решение. В системе отсчета (с.о.) «сосуд» все молекулы получат приращение скорости  (рис. 20.8). Выясним, какой станет при этом средняя кинетическая энергия молекул в с.о. «сосуд». (рис. 20.8). Выясним, какой станет при этом средняя кинетическая энергия молекул в с.о. «сосуд».
|
| Т¢ = ? Т² = ? | ||
 Пусть
Пусть 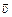 – скорость молекулы до разгона сосуда;
– скорость молекулы до разгона сосуда;  – скорость молекулы после разгона сосуда (рис. 20.9). Обозначим буквой a угол между векторами
– скорость молекулы после разгона сосуда (рис. 20.9). Обозначим буквой a угол между векторами 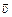 и
и  . По теореме косинусов
. По теореме косинусов
υ¢2 = υ2 + и2 + 2иυcosa.
Пусть 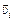 – скорость i-й молекулы до, а
– скорость i-й молекулы до, а 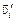 – после разгона, ai – угол между векторами
– после разгона, ai – угол между векторами  и
и  , тогда средняя кинетическая энергия молекулы в с.о. «сосуд» равна
, тогда средняя кинетическая энергия молекулы в с.о. «сосуд» равна
 =
=
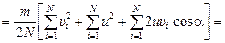
 .
.
Первое слагаемое  – это средняя кинетическая энергия молекул в с.о. «земля».
– это средняя кинетическая энергия молекул в с.о. «земля».
Второе слагаемое 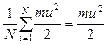 – это кинетическая энергия одной молекулы, которая движется со скоростью и.
– это кинетическая энергия одной молекулы, которая движется со скоростью и.
 Третье слагаемое
Третье слагаемое 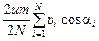 . Разберемся с ним. В силу большого числа молекул на всякую молекулу, имеющую скорость
. Разберемся с ним. В силу большого числа молекул на всякую молекулу, имеющую скорость 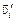 , составляющую угол
, составляющую угол 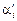 со скоростью
со скоростью  , найдется молекула (в силу симметрии задачи), летящая в противоположном направлении с такой же по величине скоростью
, найдется молекула (в силу симметрии задачи), летящая в противоположном направлении с такой же по величине скоростью 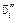 = –
= – 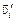 , при этом угол
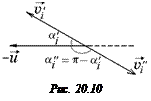
, при этом угол 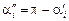 (рис. 20.10). Тогда
(рис. 20.10). Тогда
 .
.
Ясно, что
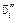 +
+ 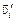 = 0,
= 0,
следовательно,
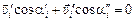 .
.
Поэтому, разбив все молекулы на такие пары, получим
 .
.
Таким образом, третье слагаемое равно нулю. Тогда
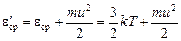 .
.
Поскольку  , то
, то 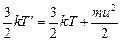 , тогда
, тогда
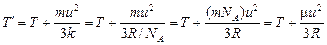 .
.
Итак,
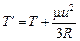 . (20.10)
. (20.10)
При торможении произойдет то же самое, что и при разгоне: все молекулы получат дополнительное приращение скорости 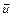 , и температура газа опять повысится:
, и температура газа опять повысится:
 .
.
Ответ: 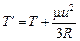 ;
; 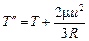 .
.
Вывод: чтобы нагреть воздух в банке, достаточно ее хорошо потрясти.
Задача 20.8. На сколько повысится температура баллона с кислородом после его удара о землю при падении с высоты h = 5 м?
| h = 5 м m = 0,032 кг/моль | Решение. Согласно формуле (20.10)
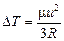 ,
и = ,
и = 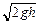 = 10 м/с. = 10 м/с.
|
| DТ = ? | |
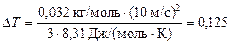 К
К
Ответ: DТ = 0,125 К.
Задача 20.9. Сосуд с газом разогнали до скорости и двумя способами: 1) сообщив скорость и одним резким ударом; 2) сначала увеличили скорость на и/2, а после того как в сосуде установилось термодинамическое равновесие, еще раз увеличили скорость на и/2. Молярная масса газа m. Найти изменение температуры в газе в обоих случаях.
| и m | Решение. Применяем формулу (20.10):
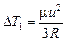 ; ; 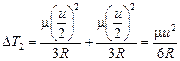 . .
|
| DТ1 = ? DТ2 = ? | |
Ответ: 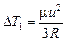 ;
;  .
.
Заметим, что в данном случае DТ1 : DТ2 = 2.
Вывод: при резком толчке температура повышается сильнее, чем при постепенном разгоне.
СТОП! Решите самостоятельно: С7, D6.
Задача 20.10.Газ находится при температуре Т. Масса молекулы газа т. Найти: 1) среднее значение проекции скорости <υх> на произвольную ось х; 2) квадрат среднего значения проекции скорости 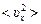 на ось х.
на ось х.
| Т т |  Рис. 20.11
Рис. 20.11
| Решение. 1. В силу симметрии на всякую молекулу, имеющую проекцию скорости υх, находится молекула, имеющая проекцию скорости (–υх) (рис. 20.11). Тогда
<υх> =  = 0. = 0.
|
<υх> = ?
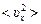 = ? = ?
| ||
2. Для всякой молекулы ее скорость υ по модулю равна
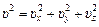
как диагональ прямоугольного параллелепипеда (рис. 20.12). Тогда


или 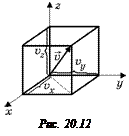
 .
.
Поскольку направления х, у и z совершенно равноправны, то
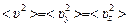 .
.
Отсюда
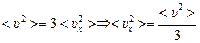 .
.
Так как 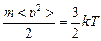 , то
, то 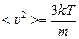 , тогда
, тогда
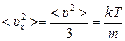 .
.
Ответ: <υх> = 0;  .
.
СТОП! Решите самостоятельно: D1, D5.
Дата добавления: 2016-04-11; просмотров: 846;
