Поверхностное натяжение некоторых жидкостей
| Жидкость | t, °С | Поверхностное натяжение, Н/м |
| Гелий (Не) | –269 | 0,00012 |
| Водород (Н2) | –253 | 0,0021 |
| Эфир | 0,017 | |
| Спирт | 0,022 | |
| Раствор мыла в воде | 0,040 | |
| Вода чистая | 0,0725 | |
| Ртуть | 0,470 | |
| Золото | 1,102 |
Заметим, что у легко испаряющихся жидкостей величина s мала.
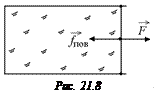
Задача 21.1.Рамка с подвижной перемычкой затянута мыльной пленкой (рис. 21.8). Длина перемычки l = 5 см. Чтобы удержать пленку, необходимо приложить силу F = 4×10–3 Н. Найти поверхностное натяжение пленки.
| l = 5 см F= 4×10–3 Н | Решение. Заметим, что мыльная пленка имеет две поверхности! Сила, с которой пленка действует на перемычку, равна силе, с которой натянута пленка – иначе бы пленка разорвалась. |
| s = ? | |
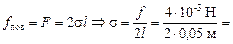
= 0,04 Н/м.
Ответ: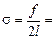 
0,04 Н/м.
Как зависит поверхностное натяжение
От температуры?
Экспериментально установлено, что с повышением температуры поверхностное натяжение уменьшается. Для примера в табл. 21.2 показана зависимость от температуры поверхностного натяжения воды.
Заметим, что от размеров и формы поверхности коэффициент поверхностного натяжения никак не зависит.
СТОП! Решите самостоятельно: А1, А4, В1, В2.
Поверхностная энергия
Поскольку при сокращении своей поверхности жидкость совершает работу, можно ввести понятие поверхностной энергии.
Величину поверхностной энергии надо определить так, чтобы убыль этой энергии была равна работе сил поверхностного натяжения при уменьшении площади поверхности жидкости.
Поверхностной энергией жидкости, имеющей поверхность S и поверхностное натяжение s, называется величина
W = sS.
Поверхностная энергия – это потенциальная энергия. Покажем, что работа сил поверхностного натяжения равна убыли потенциальной энергии: А = W1 – W2 = –DW.
Возьмем рамку с подвижной невесомой перемычкой длины l, затянутой жидкой пленкой. Полная поверхность пленки в начальный момент равна S1= 2bl. Напомним, что множитель «2» появляется потому, что пленка имеет две поверхности.
Поверхностная энергия
W1 = sS1 = 2bls.
Пусть под действием сил поверхностного натяжения перемычка сместится на Dх (рис. 21.9). Тогда площадь уменьшится на 2lDх:
S2= S1 – 2lDх,
W2 = sS2 = s(2bl – 2lDх).
Убыль поверхностной энергии
W1 – W2 = 2bls – s(2bl – 2lDх) = 2lDхs.
Работа сил поверхностного натяжения
А = FDx = 2lDхs.
Итак,
А = W1 – W2 = –DW .
Значит, мы правильно (т.е. удобно) для нас ввели величину поверхностной энергии W. Зная разность энергий в начале и конце процесса, можно вычислить работу сил поверхностного натяжения.
Заметим, что из формулы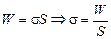 
, то есть поверхностное натяжение можно определить как энергию, которой обладает поверхность жидкости единичной площади. Итак,
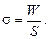(21.2)
Тогда
.
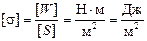Задача 21.2. Деревянная палочка плавает на поверхности воды. По одну сторону от палочки осторожно налили мыльный раствор (рис. 21.10). Что произойдет?
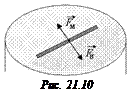Решение. Сила, действующая на палочку со стороны мыльного раствора, равна
Fм = sмl,
а со стороны воды
Fв = sвl.
Так как sв > sм (см. табл. 21.1), то палочка будет двигаться от границы «вода – мыльный раствор» в сторону воды. (Не верите? Проверьте экспериментально.)
СТОП! Решите самостоятельно: А2, А3, В3.
Задача 21.3. Две капли ртути радиусом R = 1,0 мм слились в одну. Сколько при этом выделилось тепла?
| R = 1,0 мм = = 1,0×10–3 м s = 0,47 Н/м | Решение. Q = W1 – W2.
W1 = sS1 = s×2×4pR2; W2= sS2 = s×4p  .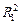
Так как объем ртути после слияния капель не изменился, то
Vдо = Vпосле =  .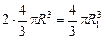
|
| Q = ? | |
Отсюда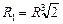 
. Тогда
Q = W1 – W2 = sS1 – sS2 = s×2×4pR2 – s4p =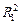
= s×8pR2 – s×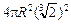 
= 
= 
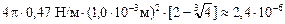Дж = 2,4 мкДж.
Ответ: 
2,4 мкДж.
СТОП! Решите самостоятельно: В7, В10, В12.
Задача 21.4. Пипетка имеет кончик диаметра D = 0,50 мм. Какова масса капли воды, оторвавшейся от пипетки?
| D = 0,50 мм = 5,0×10–4 м s = 0,0725 Н/м | Решение. При отрыве капли силы поверхностного натяжения направлены вертикально вверх и равны |
| т = ? |
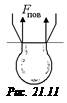Fпов = pDs.
Условия отрыва капли Fпов = mg. Тогда
Fпов = mg = pDs Þ 
.
Подставим численные значения:
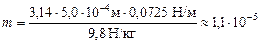кг = 1,1×10–2 г = 11 мг.
Ответ: » 11 мг.
СТОП! Решите самостоятельно: В4, В5, В6.
Дата добавления: 2016-04-11; просмотров: 1056;