Капиллярные явления
Капиллярами называются узкие трубки диаметра менее 1 мм.
Рассмотрим экспериментальные факты. Опустим в широкий сосуд с жидкостью капилляр. Если жидкость не смачивает капилляр, уровень в капилляре будет ниже уровня жидкости в сосуде (рис. 22.3,а), если смачивает – уровень будет выше (рис. 22.3,б). Поверхность жидкости в капилляре в обоих случаях будет изогнутой.
Рис. 22.3 
Изогнутые поверхности жидкости в капиллярах называются менисками.
СТОП! Решите самостоятельно: А1–А4, В2, В3, С1–С3.
Угол, который образует касательная к поверхности жидкости со стенкой капилляра, называется краевым углом.
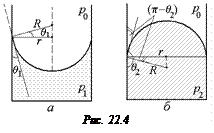 Для смачивающих жидкостей (рис. 22.4,а) краевой угол
Для смачивающих жидкостей (рис. 22.4,а) краевой угол
0 £ q1 £  .
.
Для несмачивающих жидкостей (рис. 22.4,б) краевой угол
 £ q2 £ p.
£ q2 £ p.
Читатель: Почему жидкость в капиллярах поднимается при смачивании или опускается при несмачивании?
Автор: Дело в том, что поверхность мениска имеет сферическую форму, и это вызывает дополнительное капиллярное давление (как в капле воды). Когда поверхность сферы выпуклая, давление в капилляре увеличивается на величину 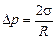 , где R – радиус сферической поверхности мениска. Когда мениск вогнутый, то давление уменьшается на эту величину.
, где R – радиус сферической поверхности мениска. Когда мениск вогнутый, то давление уменьшается на эту величину.
Задача 22.1. Взяли два капилляра радиуса r. В один капилляр налили смачивающую жидкость с поверхностным натяжением s1, а в другой – несмачивающую с поверхностным натяжением s2. Давление воздуха р0. Краевые углы равны соответственно q1 < 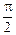 и q2 >
и q2 > 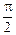 . Давление воздуха р0. Найти давление под поверхностями менисков в обоих случаях.
. Давление воздуха р0. Найти давление под поверхностями менисков в обоих случаях.
| r р0 s1 s2 q1 q2 | Решение. Обозначим радиус мениска через R.
1. Из рис. 22.4,а видно, что r = Rcosq1. Тогда
 ; Dр = ; Dр = 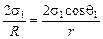 ;
р1 = р0 – Dр = р0 – ;
р1 = р0 – Dр = р0 – 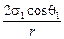 .
2. Из рис. 22.4,б видно r = Rcos(p – q2). Тогда .
2. Из рис. 22.4,б видно r = Rcos(p – q2). Тогда
|
| р1 = ? р2 = ? |
 ; Dр =
; Dр =  ;
;
р2 = р0 + Dр = р0 + 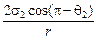 = р0 –
= р0 –  .
.
Ответ: р1 = р0 – 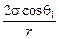 ; р2 = р0 –
; р2 = р0 –  .
.
Итак, запомним, что для любого краевого угла справедливо: давление под поверхностью мениска равно
р = р0 – 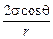 . (22.1)
. (22.1)
При этом при острых краевых углах q р < р0; при тупых краевых углах q р > р0.
Задача 22.2. Два капилляра радиуса r опущены в сосуд с жидкостями (рис. 22.5): первый – в смачивающую с поверхностным натяжением s1 и краевым углом q1 < 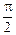 ; второй – в несмачивающую с поверхностным натяжением s2 и краевым углом
; второй – в несмачивающую с поверхностным натяжением s2 и краевым углом 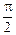 < q < p. На сколько поднимется (опустится) жидкость в этих капиллярах?
< q < p. На сколько поднимется (опустится) жидкость в этих капиллярах?
r
s1, s2
q1 < 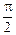
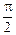 < q < p < q < p
|  Рис. 22.5
Рис. 22.5
|
| h1 = ? h2 = ? | |
Решение. 1. Случай q1 < 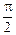 . Рассмотрим уровень жидкости О–О (рис. 22.5,а). Давление в капилляре в точке А равно давлению снаружи капилляра на поверхности жидкости, т.е. атмосферному давлению. Тогда давление в точке А внутри капилляра складывается из давления р1 под поверхностью мениска, которое определяется формулой (22.1), и гидростатического давления столба жидкости высотой h1:
. Рассмотрим уровень жидкости О–О (рис. 22.5,а). Давление в капилляре в точке А равно давлению снаружи капилляра на поверхности жидкости, т.е. атмосферному давлению. Тогда давление в точке А внутри капилляра складывается из давления р1 под поверхностью мениска, которое определяется формулой (22.1), и гидростатического давления столба жидкости высотой h1:
р0 = р0 –  + ρgh1.
+ ρgh1.
Отсюда
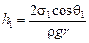 . (22.2)
. (22.2)
2. Случай 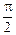 < q < p. Рассмотрим уровень жидкости O¢–O¢ (рис. 22.5,б). Давление в капилляре в точке В равно давлению снаружи р0 + ρgh2 = р, где р определяется по формуле (22.1):
< q < p. Рассмотрим уровень жидкости O¢–O¢ (рис. 22.5,б). Давление в капилляре в точке В равно давлению снаружи р0 + ρgh2 = р, где р определяется по формуле (22.1):
р0 + ρgh2 = р0 –  .
.
Отсюда
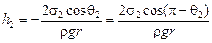 > 0 (соsq2 < 0).
> 0 (соsq2 < 0).
Ответ: 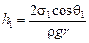 ;
; 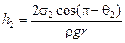 .
.
СТОП! Решите самостоятельно: А5–А7, В4, В5, В11, С6.
Дата добавления: 2016-04-11; просмотров: 731;
