Под цилиндрической поверхностью

Если каплю ртути сжать между двумя стеклянными пластинами, она расплющится «в лепешку», края которой будут близки к цилиндрической поверхности малого радиуса. Оценим, какое дополнительное давление дает в этом случае мениск цилиндрической формы.

Задача 22.7. Слой несмачивающей жидкости зажат между двумя плоскостями. Длина слоя l. Край жидкости имеет цилиндрическую поверхность радиуса R (рис. 22.10). Краевой угол q = 180°. Найти избыточное давление в жидкости.

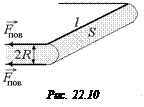Эти силы обусловливают давление на площадь S = 2Rl. Следовательно, избыточное давление, создаваемое ими, равно

.

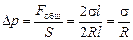Ответ:

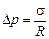. (22.4)

Итак, давление в расплющенной капле несмачивающей жидкости будет выше атмосферного.

Читатель: А если расплющить каплю смачивающей жидкости, например воды?

Автор: Вода сама «рада» расплющиться! Поскольку она смачивает стекло, избыточное давление будет отрицательным. То есть давление в расплющенной капле воды будет равно р = р₀ – 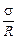, где s – поверхностное натяжение воды, R = d/2 – половина расстояния между стенками. Это значит, что стекла будут притягиваться!

Задача 22.8. Между двумя стеклянными пластинами расплющена капля воды. Считается, что расстояние между пластинами d = = 0,0010 мм, а площадь капли S = 10 см². Определить минимальную силу, которую надо приложить к стеклам, чтобы их разделить.

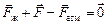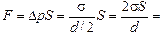
d = 0,0010 мм = = 1,0×10–6 м S = 10 см2 = = 10×10–4 м2 s = 0,0725 Н/м	Решение. Прикрепим одно из стекол к стенке, а другое будем пытаться оторвать от первого силой F (рис. 22.11). Условие отрыва стекла имеет вид , где Fж = (p0 – Dp)S; Fатм = p0S; F – искомая величина. Запишем это же уравнение в проекции на горизонтальную ось х: (р0 – Dp)S + F – p0S = 0. Тогда 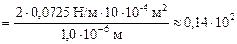Н = = 0,14 кН.
F = ?
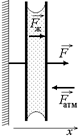Рис. 22.11

Очень приличная сила!

Ответ: 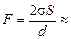0,14 кН.

СТОП! Решите самостоятельно: С10, С11.