Поверхностью жидкости
Читатель: Что больше: давление жидкости в капле воды, находящейся в воздухе, или атмосферное давление?
Автор: Силы поверхностного натяжения «стягивают» каплю так, как если бы она находилась в упругой эластичной оболочке. Поэтому давление внутри капли должно быть больше атмосферного.
Задача 21.5. Найти разность давлений внутри и снаружи капли воды радиуса r, если поверхностное натяжение равно s.
| r s | Решение. Мысленно рассечем сферическую каплю радиуса R плоскостью на два полушария (рис. 21.12). Из-за поверхностного натяжения слои полушарий притягиваются друг к другу с силой F = 2pRs. Эта сила прижимает полушария друг к другу по поверхности площади S = pR2 и, следовательно, создает дополнительное давление
 .
Ответ:
|
| Dр = ? | |
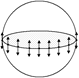Рис. 21.12
|
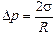. (21.3)
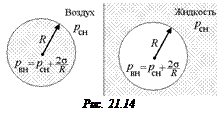
Читатель: Внутри жидкости находятся пузырьки воздуха сферической формы (рис. 21.13). Что больше: давление в жидкости или давление в пузырьке?
| Автор: Если пузырек увеличит свою поверхность, то возрастет площадь поверхности раздела «жидкость – воздух». На увеличение этой площади требуется затратить энергию, т. е. вода будет препятствовать расширению пузырька. Значит, силы поверхностного натяжения воды сжимают пузырек, и давление в нем больше, чем в жидкости. |
Рис. 21.13
|
Задача 21.6. Жидкость граничит с воздухом так, что граница раздела «жидкость – воздух» имеет форму сферы. Доказать, что разность давлений внутри и снаружи сферы
,
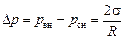где s – поверхностное натяжение, R – радиус сферы.
Решение. Результат доказательства не зависит от того, рассматриваем ли мы каплю воды в воздухе или пузырек воздуха в воде (рис. 21.14). Мысленно добавим чуть-чуть воздуха в пузырек и чуть-чуть жидкости в каплю так, чтобы пузырек или капля увеличили свой радиус на DR << R. Считаем, что Т = const, р » const.
Тогда для обоих случаев работа, произведенная за счет наших добавок, составит
DA = (рвн – рсн)SDR = Dp×4pR2DR.
По своей сути – это работа внешних сил, которая идет на увеличение энергии системы. Поверхностная энергия увеличилась на величину
DW = sDS = s[S2 – S1] = s[4p(R + DR)2 – 4pR2] = 8pRDRs.
Можно утверждать, что DА = DW, так как работа внешних сил равна увеличению энергии системы.
Следовательно,
Dp×4pR2DR = 8pRDRs Þ .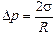
Ответ: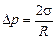 
.
Как видим, и для капли и для пузырька один и тот же результат!
Задача 21.7.Найти давление в капле воды радиуса R1 = 1,00´ ´10–6 м, образующей туман, и избыточное давление внутри капли ртути радиуса R2 = 1,0×10–3 м. Коэффициент поверхностного натяжения воды s1 = 0,0725 Н/м, ртути s2 = 0,47 Н/м. Атмосферное давление р0 = 1,00×105 Па.
| R1 = 1,00×10–6 м R2 = 1,0×10–3 м s1 = 0,0725 Н/м s2 = 0,47 Н/м р0 = 1,00×105 Па | Решение. Воспользуемся формулой (21.3) и учтем, что давление в капле тумана – это сумма атмосферного давления и давления сил поверхностного натяжения капли:
р1 = р0 + Dр1 =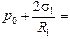 
= 1,00×105 Па +  Па.
|
| р1 = ? Dр2 = ? | |
Для ртути
Dр2 =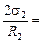 
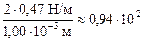Па = 0,94 кПа.
Ответ: р1 =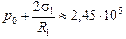 
Па; Dр2 = 
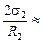0,94 кПа.
СТОП! Решите самостоятельно: В11, С2.
Задача 21.8. Найти избыточное давление воздуха внутри мыльного пузыря радиуса R = 1,0×10–3 м, если s = 0,040 Н/м.
| R = 1,0×10–3 м s = 0,040 Н/м | Решение. В силу того, что толщина мыльного пузыря очень мала, можно считать, что внешний и внутренний радиусы пузыря равны (рис. 21.15). Внутри мыльной пленки давление равно |
| Dр = ? |
р1 = р0 + Dр = р1 +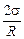 
,
где р0 – давление снаружи.
Внутри пузыря давление
р2 = р1 + Dр = р1 + =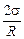
=  .
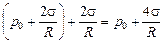Давление внутри сферы всегда больше давления снаружи на  .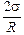
Итак,
| 
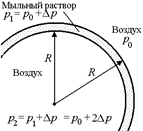Рис. 21.15
|
= 
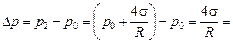
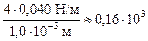Па = 0,16 кПа.
Ответ: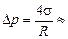 
0,16 кПа.
Заметим, что чем меньше мыльный пузырь, тем больше в нем избыточное давление.
СТОП! Решите самостоятельно: А8, А9, В13.
Дата добавления: 2016-04-11; просмотров: 2092;