Взаимно нерастворимые жидкости
Теперь обратимся к смесям таких веществ, которые практически нераство-
римы друг в друге. Примеры — вода—масло, вода—бензол.
1. Подобные смеси имеют две принципиальные особенности.
а) Первая: так как и в смеси жидкости находятся в виде однородных мультимолекулярных структур (например, в виде капель из молекул одного типа), то присутствие одной жидкости не влияет на давление пара другой (в отличие от взаимно растворимых жидкостей). Т.е., независимо от состава смеси давление пара каждого компонента — то же, что и для чистого компонента, — 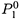 и
и 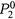 .
.
б) Но пузырьки пара, образующиеся при закипании смеси, содержат пары обоих веществ. Поэтому закипание наступает тогда, когда с внешним давлением
сравняется общее давление обоих паров: 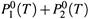 .
.
 |
Отсюда вытекает вторая особенность: температура кипения смеси ниже
температуры кипения любого компонента
Для взаимно же растворимых жидкостей (исключая азеотропные смеси) температура кипения смеси, как видно из диаграммы рис. 9.4, находится в интервале
между температурами кипения отдельных компонентов:
 |
2. Приведем конкретный пример. У воды и у скипидара давление паров
достигает атмосферного, соответственно, при следующих температурах:
 |
а совокупное давление паров этих веществ сравнивается с атмосферным при
 |
(в широком диапазоне состава смеси); т.е., действительно, смесь закипает при более низкой температуре, чем любой чистый компонент.
3. а) На указанной особенности основан метод очистки органических жидкостей от примесей — перегонка с водяным паром. Дело в том, что многие органические вещества при своей температуре кипения разлагаются. Поэтому их смешивают с водой. Температура кипения становится ниже, чем даже у воды, и органическое вещество уже выдерживает кипячение.
б) Последовательность операций такова. Вначале смесь испаряют (при этом
загрязняющие вещества в пар не переходят). Затем пар конденсируют; образующаяся жидкая фаза расслаивается на две фазы — воду и органическую
жидкость. Вторую фазу осторожно отделяют.
4. Каково соотношение компонентов смеси в паре?
 |
а) Учтем, что испарение производят в некотором фиксированном (постоянном) объеме V. И запишем уравнение Клайперона—Менделеева для компонентов в газообразном состоянии:
Отсюда видно, что в образующемся паре количество компонента пропорционально давлению его насыщенного пара при данной температуре.
 |
б) Кроме того, нетрудно найти массовую долю компонента в паре:
в) После подстановки 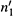 и
и 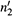 получаем:
получаем:
 |
Если 1 — H2O, а 2 — очищаемая жидкость, то видно: массовая доля этой жидкости в паре тем больше, чем больше отношение 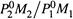 ..
..
Экстракция
1. Система взаимно нерастворимых жидкостей позволяет осуществить еще одну важную процедуру — экстракцию. Речь идет уже о трехкомпонентной системе: она включает две несмешивающиеся жидкости и распределенный между ними третий компонент (рис. 10.3).
 2. а) При равновесии химические потенциалы этого компонента в двух фазах одинаковы:
2. а) При равновесии химические потенциалы этого компонента в двух фазах одинаковы:
б) Отсюда
т.е. отношение активностей третьего компонента в фазах не зависит от общего количества этого компонента в фазах.
Здесь γi – коэффициенты активности, а через К обозначается термодинамическая константа распределения. Она, как любая константа равновесия, зависит от температуры и давления.
 |
в)Отношение же концентраций называется коэффициентом распределения:
Коэффициент распределения зависит от концентраций, так как при их изменении могут меняться коэффициенты активности. В первую очередь это относится к электролитам.
3. Так вот, часто вещества распределяются между двумя несмешивающимися жидкостями очень неравномерно.
Это позволяет с помощью одной такой жидкости извлекать вещества из другой жидкости. Данная процедура и называется экстракцией; весьма широко она применяется в фармации. Например,
- с помощью водных сред из разных объектов извлекают водорастворимые компоненты,
- а с помощью неполярных жидкостей (например, масел, бензола, ацетона и т.д.) — соединения углеводородной природы.
4. Рассмотрим, от чего зависит эффективность экстракции.
а) Обозначим: VI — объем первой жидкости (где изначально находилось экстрагируемое вещество), VII — объем второй жидкости (с помощью которой осуществляется экстракция). И будем считать, что в обеих жидкостях коэффициенты активности вещества близки к единице: γI≈ γII ≈ 1,0.
б) Тогда при равновесии
 |
 |
в) Отсюда находим массу вещества в каждой из фаз:
Видно: чем больше К и VII, тем больше масса экстрагированного вещества (mII).
5. а) Можно осуществить и так называемую дробную экстракцию— разделить объем VII на п равных частей: экстрагировать сначала одной частью и удалить фазу II, добавить очередную порцию экстрагента, вновь ее удалить — и т.д.
б) Тогда, например, в формулах второй экстракции вместо т0 следует ставить то количество вещества, которое осталось в фазе I после первой экстракции:
 |
 |
в) Обобщая последнюю формулу, получаем выражения для массы вещества в каждой из фаз после п экстракций:
 |
г) Если продифференцировать формулу для mI,n по п, можно убедиться:
 |
Это значит, что при росте числа экстракций (при том же общем объеме экстрагента) количество вещества, остающегося в первой жидкости, становится всё меньше, т. е. дробная экстракция эффективней, чем простая.
10.4. Затвердевание бинарных жидких смесей:
Простейший случай
Теперь обратимся к затвердеванию жидких смесей.
а) Для полноты картины вначале коротко остановимся на ситуации, ког-
да компоненты неограниченно взаимно растворимы и в жидком, и в твердом
состояниях. Обычно это вещества, близкие по своей природе, — например,
Ag–Au , NaCl–NaBr и т.д. Но в каждой паре одно из веществ (1) плавится (и затвердевает) при более высокой температуре, а другое (2) — при более
низкой.
 б) В идеальном случае диаграмма плавления (рис. 10.4) имеет точно такой же вид, как диаграмма кипения идеальной смеси (см. рис. 9.4), т.е. для смеси Tпл будет зависеть от состава смеси — уменьшаться с увеличением доли в жидкой фазе
б) В идеальном случае диаграмма плавления (рис. 10.4) имеет точно такой же вид, как диаграмма кипения идеальной смеси (см. рис. 9.4), т.е. для смеси Tпл будет зависеть от состава смеси — уменьшаться с увеличением доли в жидкой фазе 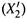 легкоплавкого компонента. Это изображено верхней кривой диаграммы — линией ликвидуса.
легкоплавкого компонента. Это изображено верхней кривой диаграммы — линией ликвидуса.
в) В кристаллах, образующихся при охлаждении смеси до Tпл , тоже содержатся оба компонента (так как они взаиморастворимы и в твёрдом состоянии), но второго (более легкоплавкого) компонента меньше (X2 < X2′). Соответственно, можно построить и линию солидуса (нижняя линия на диаграмме): она связывает состав твёрдой фазы с Tпл.
г) Как и для перехода 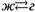 , здесь тоже возможны другие варианты диаграммы плавления, в т.ч. с экстремумами на кривых ликвидуса и солидуса. Например, для смеси Cu-Au наблюдается минимум на этих линиях.
, здесь тоже возможны другие варианты диаграммы плавления, в т.ч. с экстремумами на кривых ликвидуса и солидуса. Например, для смеси Cu-Au наблюдается минимум на этих линиях.
Следовательно, справедливо то, что говорилось об азеотропной смеси: в точке экстремума составы жидкой и твердой фаз одинаковы.
Дата добавления: 2016-03-20; просмотров: 3406;
