Длина свободного пробега
Задача 20.10. Оценить среднюю длину свободного пробега молекулы газа. Считать молекулы шарообразными диаметра d, концентрация молекул п.
| d n | Решение. Сделаем упрощающее предположение: будем считать, что движется только выделенная нами молекула, а все остальные молекулы застыли неподвижно на своих местах. |
| l= ? | |
Ударившись об одну из неподвижных молекул, выделенная молекула будет лететь прямолинейно и равномерно до тех пор, пока не столкнется с другой неподвижной молекулой. Это произойдет в том случае, если центр неподвижной молекулы окажется от прямой, вдоль которой летит молекула, на расстоянии, меньшем диаметра d (рис. 20.13).
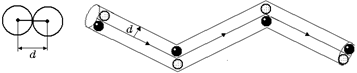
Рис. 20.13
В результате соударения молекула изменит направление своего движения, после чего опять будет двигаться прямолинейно и равномерно, пока на ее пути снова не встретится молекула, центр которой находится внутри показанного на рисунке коленчатого цилиндра радиуса d.
Число столкновений за время t равно числу молекул, попавших внутрь этого цилиндра, объем которого образуется движением молекул со скоростью υ за время t и равен
.
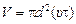Число молекул в этом объеме
.
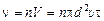Время между двумя столкновениями
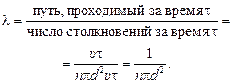
Ответ:
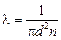. (20.11)
Заметим, что на самом деле, так как все молекулы движутся, полученное нами значение l завышено. Относительная скорость движения молекул выше, чем средняя скорость молекулы. Поэтому точное значение
.
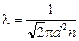Дата добавления: 2016-04-11; просмотров: 592;