Учет линейно-вязкого сопротивления при вынужденных колебаниях систем с конечным числом степеней свободы.
При учете линейно-вязкого сопротивления дифференциальное уравнение движения механической системы записывается в виде
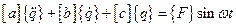 . (3.20)
. (3.20)
Здесь 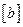 - матрица обобщенных коэффициентов демпфирования. Нас будут интересовать установившиеся вынужденные колебания, поэтому будем разыскивать только частное решение уравнения (3.20), которое представим в виде
- матрица обобщенных коэффициентов демпфирования. Нас будут интересовать установившиеся вынужденные колебания, поэтому будем разыскивать только частное решение уравнения (3.20), которое представим в виде
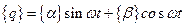 (3.21)
(3.21)
Если принять эту форму за основную, то легко найти скорость и ускорение
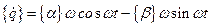 (3.22)
(3.22)
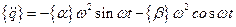 (3.23)
(3.23)
Подставляя (3.21) - (3.23) в дифференциальное уравнение (3.20) и приравнивая коэффициенты, стоящие при одноименных тригонометрических функциях, приходим к системе алгебраических уравнений относительно векторов 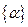 и
и 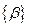
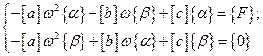
или
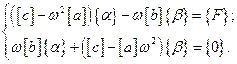
Используя блочные матрицы, эту систему уравнений можно записать так
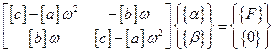
В результате ее разрешения относительно матриц - столбцов 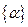 и
и 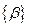 можно вычислить амплитуды вынужденных колебаний для каждой обобщенной координаты по формуле
можно вычислить амплитуды вынужденных колебаний для каждой обобщенной координаты по формуле
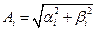 .
.
Законы изменения обобщенных координат записываются в форме
 .
.
Здесь 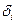 - начальная фаза колебаний, соответствующая
- начальная фаза колебаний, соответствующая 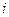 -ой обобщенной координате, она может быть вычислена по формуле
-ой обобщенной координате, она может быть вычислена по формуле
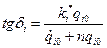 .
.
ПРИМЕР 7. Найти закон вынужденных колебаний механической системы, представленной на рис.3.15, используя главные координаты. Все необходимые величины указаны на рисунке.
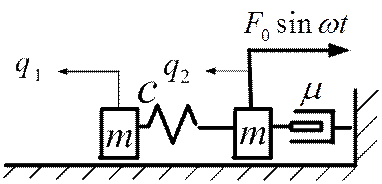
Рис. 3.15
РЕШЕНИЕ. В качестве обобщенных координат выбираем координаты материальных точек и записываем их в виде двухкомпонентного вектора состояния
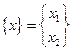
1. Вычисляем кинетическую энергию
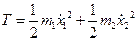
и подсчитываем обобщенные коэффициенты инерции:
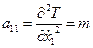 ;
; 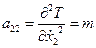 ;
; 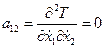 .
.
После чего можно записать выражение для матрицы инерции
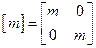 .
.
Вычисляем потенциальную энергию системы
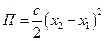 .
.
Вычислив обобщенные коэффициенты жесткости
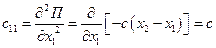 ;
; 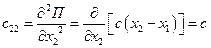 ;
;
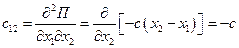 ,
,
получим выражение для матрицы жесткости
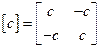 .
.
2. Чтобы записать решение в главных координатах необходимо построить матрицу преобразований, а для этого нудно найти формы собственных колебаний. Переходим к определению собственных частот и форм колебаний, для чего запишем уравнение свободных колебаний системы:
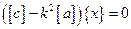 . (3.24)
. (3.24)
Предполагаем, что решение этого уравнения имеет вид
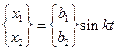 .
.
После его подстановки в уравнение (3.24) получаем систему алгебраических уравнений:
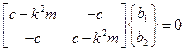 .
.
Запишем частотное уравнение
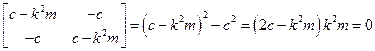
и найдем его корни (собственные частоты), полагая 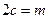 . Тогда
. Тогда
 ,
, 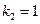 .
.
Находим нормированные формы собственных колебаний:
для первой собственной частоты  имеем
имеем
 ,
, 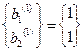 - нормированная форма;
- нормированная форма;
для второй собственной частоты 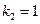
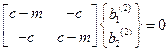 ,
, 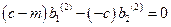 ,
, 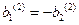 ,
,
и окончательно
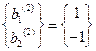 - нормированная форма.
- нормированная форма.
3. Построим матрицу преобразований для перехода к главным координатам:
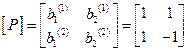 .
.
4. Перейдем к построению структуры уравнения вынужденных колебаний с учетом сопротивления. Запишем силовое воздействие в матричной форме:
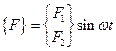 .
.
Его элементы вычисляем как обобщенные силы, соответствующие вариациям обобщенных координат 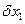 и
и 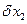
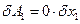 ;
; 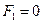 ;
;
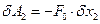 ;
; 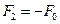 ,
,
поэтому
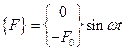 .
.
Уравнения вынужденных колебаний с учетом сопротивления можно записать с помощью блочной матрицы
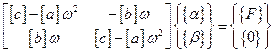 .
.
Или развернутом виде
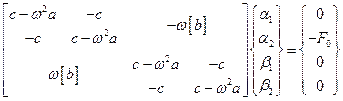 . (3.25)
. (3.25)
Построим матрицу сил сопротивления 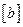 .
.
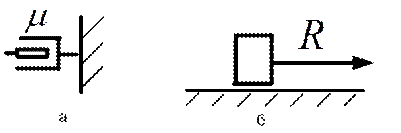
Рис.3.16
Демпфирующий элемент (рис.3.16.а) заменим силовым воздействием (рис.3.16.б), пропорциональным скорости 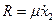 . Компонентами матрицы сил сопротивлении являются обобщенные силы сопротивления, определенные на возможных перемещениях
. Компонентами матрицы сил сопротивлении являются обобщенные силы сопротивления, определенные на возможных перемещениях 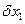 и
и 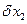 . Вычислим их
. Вычислим их
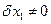 и
и 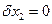 :
: 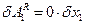 ;
; 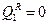 ,
,
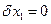 и
и 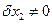 :
: 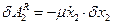 ;
; 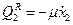 .
.
Теперь легко построить матрицу сил сопротивления
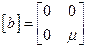 . (3.26)
. (3.26)
Учитывая (3.26) запишем уравнения вынужденных колебаний (3.25) с учетом сопротивления в окончательном виде
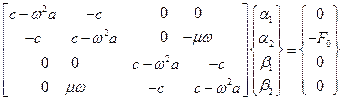 .
.
Используя матрицу преобразований, переходим к главным координатам
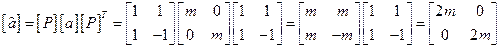 ;
;
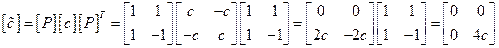 .
.
Матрица 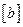 может быть построена как функция Релея. Для одного вязкого элемента (рис.3.14. а) функция Релея определяется по формуле.
может быть построена как функция Релея. Для одного вязкого элемента (рис.3.14. а) функция Релея определяется по формуле.
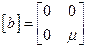 .
.
Переходя к главным координатам, преобразуем матрицу 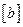
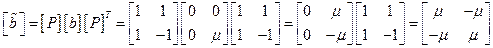 .
.
Силовое воздействие в главных координатах записывается в форме
 .
.
5. Записываем уравнение вынужденных колебаний с учетом сопротивления в главных координатах
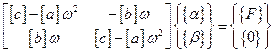 ,
,
или в развернутом виде
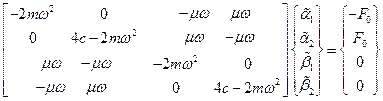 .
.
Решая это матричное уравнение можно найти амплитудные значения обобщенных координат: 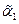 ,
, 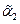 ,
, 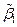 ,
, 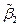 .
.
Дата добавления: 2016-02-11; просмотров: 1025;
