Cемейство окружностей постоянной активной части входного сопротивления: .

На рис. 12.3.1 показаны некоторые из этих окружностей, соответствующие положительным значениям 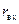(для пассивных цепей активная часть сопротивления неотрицательна). На действительной оси нанесены точки 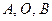из векторной диаграммы рис. 12.2.1, что позволяет совместить круговую и векторную диаграммы и оправдать данное выше определение круговой диаграммы. Как видно из рисунка, окружности постоянных 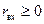целиком лежат внутри круга единичного радиуса. Как отмечено выше, окружности постоянных 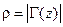также лежат внутри единичного круга, но их центры лежат в точке (0, 0). Таким образом, дробно-линейное преобразование (12.1.5) отображает правую полуплоскость комплексной переменной 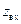на внутреннюю область единичного круга 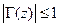, лежащего в плоскости комплексной переменной 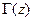. Все окружности постоянного 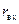касаются друг друга в точке 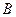холостого хода с координатами 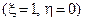. 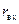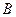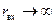Точки центров окружностей постоянного сгущаются к точке при , что ограничивает точность графических построений при .

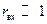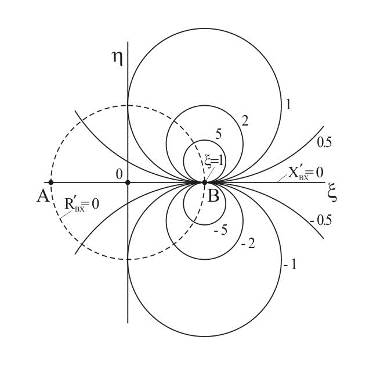
Перейдем к окружностям постоянной реактивной части входного сопротивления: 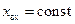, уравнение каждой такой окружности дается (12.3.3), если считать 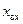постоянной. Представив уравнение (12.3.3) в виде

,

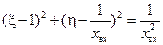и сравнивая его с (12.3.4), находим, что на комплексной плоскости 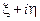центр окружности постоянного 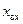находится в точке 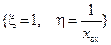, а ее радиус равен 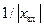. При 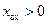(индуктивный характер входного сопротивления) центры находятся в верхней полуплоскости, при 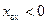(емкостной характер входного сопротивления) – в нижней полуплоскости.