Векторная диаграмма полных напряжения и тока в различных сечениях линии
Как следует из (12.1.2), числитель 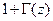 формулы (12.1.4) в некотором относительном масштабе пропорционален комплексной амплитуде напряжения в точке
формулы (12.1.4) в некотором относительном масштабе пропорционален комплексной амплитуде напряжения в точке 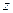 , а знаменатель – комплексной амплитуде тока в точке
, а знаменатель – комплексной амплитуде тока в точке 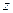 . На рис. 12.2.1 а) из т. А на комплексной плоскости проведен вектор единичной длины, соответствующий в выбранном масштабе комплексной амплитуде падающей волны при
. На рис. 12.2.1 а) из т. А на комплексной плоскости проведен вектор единичной длины, соответствующий в выбранном масштабе комплексной амплитуде падающей волны при 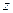 =0 (для определенности фаза вектора при
=0 (для определенности фаза вектора при 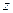 =0 выбрана нулевой). Точка конца вектора
=0 выбрана нулевой). Точка конца вектора 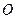 есть центр окружности, по которой движется конец вектора
есть центр окружности, по которой движется конец вектора 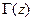 . Прибавляя к построенному вектору вектор
. Прибавляя к построенному вектору вектор 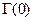 и вектор
и вектор 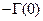 , получаем в выбранном масштабе вектор
, получаем в выбранном масштабе вектор 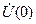 и вектор
и вектор 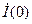 . При выбранном для построения диаграммы направлении
. При выбранном для построения диаграммы направлении 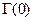 напряжение опережает по фазе ток, значит, тем самым был выбран индуктивный характер нагрузки.
напряжение опережает по фазе ток, значит, тем самым был выбран индуктивный характер нагрузки.
Будем увеличивать 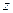 до тех пор, пока вектор
до тех пор, пока вектор 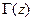 не примет направления, показанного на рис. 12.2.1 б), т. е. станет вещественным:
не примет направления, показанного на рис. 12.2.1 б), т. е. станет вещественным: 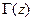 =
= 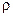 . В этом сечении линии напряжения падающей и отраженной волн сложились синфазно, т. е. имеется пучность напряжения, а токи падающей и отраженной волн – противофазно, т. е. имеется узел тока. Как видим, нормированное входное сопротивление нагруженной линии такой длины (см. (12.1.4)):
. В этом сечении линии напряжения падающей и отраженной волн сложились синфазно, т. е. имеется пучность напряжения, а токи падающей и отраженной волн – противофазно, т. е. имеется узел тока. Как видим, нормированное входное сопротивление нагруженной линии такой длины (см. (12.1.4)):
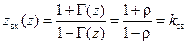 , ,
| (12.2.1) |
т. е. вещественно и равно коэффициенту стоячей волны, как и должно быть в пучности напряжения.
Увеличиваем далее 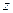 , пока конфигурация векторов не примет вид, похожий на диаграмму рис. 12.2.1 в). Теперь ток опережает по фазе напряжение, т. е. входное сопротивление носит емкостной характер. Увеличиваем далее
, пока конфигурация векторов не примет вид, похожий на диаграмму рис. 12.2.1 в). Теперь ток опережает по фазе напряжение, т. е. входное сопротивление носит емкостной характер. Увеличиваем далее 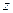 до тех пор, пока вектор
до тех пор, пока вектор 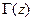 не примет направления, противоположного действительной оси (рис. 12.2.1 г)), т. е. станет вещественным отрицательным:
не примет направления, противоположного действительной оси (рис. 12.2.1 г)), т. е. станет вещественным отрицательным: 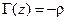 . При этом напряжения падающей и отраженной волн сложились противофазно, образуя узел напряжения, а токи падающей и отраженной волн сложились синфазно, образуя пучность тока. Нормированное входное сопротивление нагруженной линии такой длины (см. (12.1.4)):
. При этом напряжения падающей и отраженной волн сложились противофазно, образуя узел напряжения, а токи падающей и отраженной волн сложились синфазно, образуя пучность тока. Нормированное входное сопротивление нагруженной линии такой длины (см. (12.1.4)):
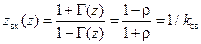 . .
| (12.2.2) |
Увеличиваем далее 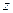 до тех пор, пока не повторится конфигурация, показанная на рис.12.2.1 а), цикл закончился, ситуация повторилась, благодаря периодичности напряжения, тока и входного сопротивления с периодом
до тех пор, пока не повторится конфигурация, показанная на рис.12.2.1 а), цикл закончился, ситуация повторилась, благодаря периодичности напряжения, тока и входного сопротивления с периодом 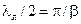 по оси
по оси 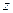 и полной окружности по вращению
и полной окружности по вращению 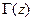 . Таким образом, на рис. 12.2.1 приведены состояния в пяти сечениях линии:
. Таким образом, на рис. 12.2.1 приведены состояния в пяти сечениях линии:
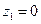 : входное сопротивление равно сопротивлению нагрузки, выбранному как комплексное индуктивного характера;
: входное сопротивление равно сопротивлению нагрузки, выбранному как комплексное индуктивного характера;
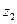 : входное сопротивление вещественно, равно КСВ;
: входное сопротивление вещественно, равно КСВ;
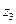 : входное сопротивление комплексное емкостного характера;
: входное сопротивление комплексное емкостного характера;
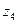 : входное сопротивление вещественно, равно 1/КСВ;
: входное сопротивление вещественно, равно 1/КСВ;
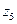 : повторяется конфигурация при
: повторяется конфигурация при 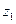 .
.
Некоторые элементы векторной диаграммы имеют специальные названия. Если отражение от нагрузки отсутствует: 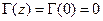 , т. е. имеется полное согласование, то концы обоих векторов
, т. е. имеется полное согласование, то концы обоих векторов 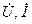 в выбранном масштабе находятся в точке
в выбранном масштабе находятся в точке  , поэтому эту точку называют точкой согласования. Если линия нагружена на КЗ, то
, поэтому эту точку называют точкой согласования. Если линия нагружена на КЗ, то 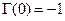 и при
и при 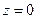 конец вектора
конец вектора 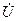 находится в точке
находится в точке 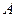 , т. е.
, т. е. 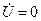 ,
, 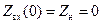 , поэтому точку
, поэтому точку 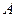 называют точкой короткого замыкания. Если линия нагружена на ХХ, то
называют точкой короткого замыкания. Если линия нагружена на ХХ, то 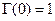 и при
и при 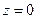 конец вектора
конец вектора 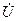 находится в точке
находится в точке 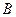 , а конец вектора
, а конец вектора 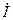 – в точке
– в точке 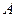 , т. е.
, т. е. 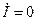 ,
, 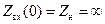 , поэтому точку
, поэтому точку 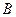 называют точкой холостого хода. Входное сопротивление при некотором
называют точкой холостого хода. Входное сопротивление при некотором 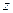 будет активным, если векторы
будет активным, если векторы 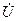 и
и 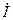 находятся на одной прямой, а такой прямой может быть только
находятся на одной прямой, а такой прямой может быть только 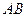 . Поэтому отрезок
. Поэтому отрезок 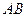 называется линией активных входных сопротивлений. Если концы векторов
называется линией активных входных сопротивлений. Если концы векторов 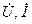 оба находятся на окружности единичного радиуса с центром в точке
оба находятся на окружности единичного радиуса с центром в точке 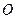 , то угол между этими векторами составляет 900, т. к. вершина угла
, то угол между этими векторами составляет 900, т. к. вершина угла 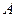 находится на окружности и он опирается на ее диаметр. В этом случае входное сопротивление чисто реактивно, поэтому указанная окружность называется окружностью чисто реактивных входных сопротивлений. Пусть нагрузка линии неизменна, а
находится на окружности и он опирается на ее диаметр. В этом случае входное сопротивление чисто реактивно, поэтому указанная окружность называется окружностью чисто реактивных входных сопротивлений. Пусть нагрузка линии неизменна, а 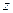 возрастает от нуля в сторону генератора. Тогда, как мы видели на рис. 12.2.1, концы векторов
возрастает от нуля в сторону генератора. Тогда, как мы видели на рис. 12.2.1, концы векторов 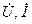 движутся по окружности радиуса
движутся по окружности радиуса 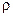 с центром в точке
с центром в точке 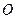 , а
, а 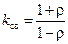 остается постоянным. Поэтому любая окружность с центром в точке
остается постоянным. Поэтому любая окружность с центром в точке 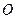 и радиусом, меньшим единицы, называется окружностью постоянного КСВ.
и радиусом, меньшим единицы, называется окружностью постоянного КСВ.
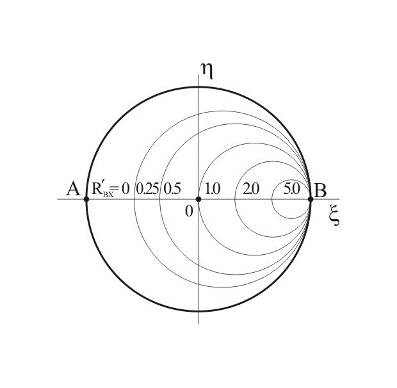
Построение круговой диаграммы
Круговая диаграмма интерпретирует соотношения (12.1.4), (12.1.5), т. е. позволяет геометрически наглядно выразить эти дробно-линейные преобразования. Более конкретно, (12.1.4) преобразует комплексную плоскость текущего коэффициента отражения 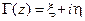 в комплексную плоскость нормированного входного сопротивления
в комплексную плоскость нормированного входного сопротивления 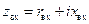 , а (12.1.5) осуществляет обратное преобразование, причем эти преобразования взаимно-однозначны. Кроме того, благодаря свойствам дробно-линейных преобразований, преобразования (12.1.4), (12.1.5) переводят окружность в окружность и сохраняют углы между пересекающимися кривыми.
, а (12.1.5) осуществляет обратное преобразование, причем эти преобразования взаимно-однозначны. Кроме того, благодаря свойствам дробно-линейных преобразований, преобразования (12.1.4), (12.1.5) переводят окружность в окружность и сохраняют углы между пересекающимися кривыми.
Пусть на плоскости 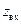 нанесена координатная сетка ортогональной прямолинейной системы координат, состоящая из двух взаимно-ортогональных семейств прямых
нанесена координатная сетка ортогональной прямолинейной системы координат, состоящая из двух взаимно-ортогональных семейств прямых 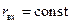 и
и 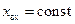 . На плоскости текущего коэффициента отражения
. На плоскости текущего коэффициента отражения 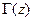 эти семейства перейдут в два взаимно-ортогональных семейства окружностей, образующих координатную сетку ортогональной криволинейной системы координат. Круговой диаграммой полных нормированных сопротивлений называется векторная диаграмма на плоскости текущего коэффициента отражения
эти семейства перейдут в два взаимно-ортогональных семейства окружностей, образующих координатную сетку ортогональной криволинейной системы координат. Круговой диаграммой полных нормированных сопротивлений называется векторная диаграмма на плоскости текущего коэффициента отражения 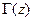 , снабженная указанной координатной сеткой. Найдем уравнения, а тем самым – положения координатных окружностей.
, снабженная указанной координатной сеткой. Найдем уравнения, а тем самым – положения координатных окружностей.
Выразим правую и левую части равенства (12.1.4) через действительные и мнимые части величин 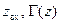 соответственно:
соответственно:
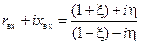 , ,
| (12.3.1) |
и приравняем по отдельности действительные и мнимые части:
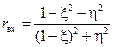 ; ;
| (12.3.2) |
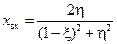 . .
| (12.3.3) |
Начнем с семейства окружностей постоянной активной части входного сопротивления: 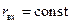 , уравнение каждой такой окружности дается (12.3.2), если считать
, уравнение каждой такой окружности дается (12.3.2), если считать 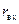 постоянной. Как известно, уравнение окружности в декартовой системе координат
постоянной. Как известно, уравнение окружности в декартовой системе координат 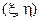 имеет вид
имеет вид
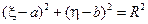 , ,
| (12.3.4) |
где 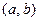 – центр окружности,
– центр окружности, 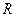 – ее радиус. Представив уравнение (12.3.2) в виде
– ее радиус. Представив уравнение (12.3.2) в виде
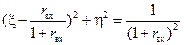 , ,
| (12.3.5) |
и сравнивая его с (12.3.4), находим, что на комплексной плоскости 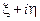 центр окружности постоянного
центр окружности постоянного 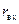 находится в точке
находится в точке 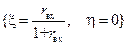 , а ее радиус равен
, а ее радиус равен 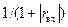 .
.
Дата добавления: 2016-02-20; просмотров: 1882;
