Составление графа ненагруженной двухпортовой цепи

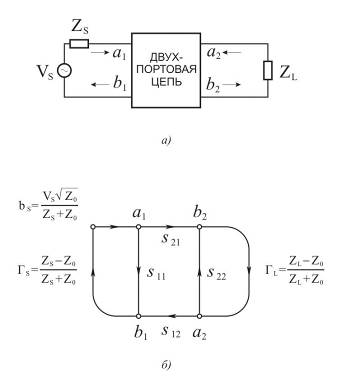
Рис. 11.3.2. Схема и граф нагруженной двухпортовой цепи.

Узлы 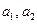соответствуют независимым переменным и являются истоками, узлы 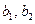– зависимым переменным и являются стоками. Напряжения от генераторов могут подаваться на вход четырехполюсника, т. е. на графе – на узел 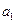, или на выход, т. е. на графе – на узел 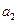, или на оба узла сразу. Направления потоков указаны стрелками, весами являются S-параметры, т. е. элементы S-матрицы четырехполюсника. Обратим внимание на генезис графа четырехполюсника (рис. 11.3.1)): первое уравнение системы представлено в виде графа на рис. 11.3.1а, наглядно показывающего, как зависимая переменная 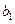представляет линейную комбинацию независимых переменных 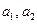; аналогично устроен подграф на рис. 11.3.1б, представляющий второе уравнение системы. Однако, для получения удобного вида объединения этих подграфов в общий граф, второй подграф «перевернут».

На рис. 11.3.2б показан граф нагруженного четырехполюсника с характеристическим сопротивлением 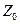; эквивалентная схема соответствующей цепи приведена на рис. 11.3.2а: слева подключен генератор с комплексной амплитудой напряжения 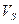и с внутренним (комплексным) сопротивлением 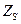,справа– нагрузка с комплексным сопротивлением 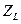. Нормированная комплексная амплитуда падающей волны от генератора

,

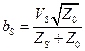(11.3.2)

формально отображена на графе узлом 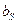; комплексный коэффициент отражения генератора

,

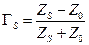(11.3.3)

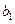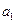формально отображен на графе ветвью от к с весом 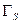; комплексный коэффициент отражения нагрузки

,

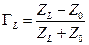(11.3.4)

формально отображен на графе ветвью от 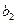к 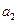с весом .

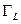В результате нагружения четырехполюсника слева и справа все четыре узла 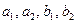становятся смешанными узлами, а это означает, что при желании граф может быть упрощен (далее техника упрощения графа путем исключения смешанных узлов не излагается, а применяется общий метод решения графа).

Решение потокового графа

В общем смысле, решение графа есть вычисление зависимых переменных по независимым переменным, или, на специфическом языке теории графов, вычисление одних узлов по другим узлам. Излагаемое ниже правило решения графа позволяет вычислять зависимые переменные, или просто узлы-стоки по одному, т. е. общее решение графа включает набор решений для индивидуальных узлов-стоков (назовем их частными решениями). Иногда нет необходимости во всех частных решениях, а нужно найти только некоторые из них, а иногда даже только одно из них. Таким образом, необходимо правило нахождения частного решения для конкретного узла-стока. Определим некоторые дополнительные термины.

Путь от одного узла к другому есть непрерывная последовательность ветвей, связывающая эти узлы, такая, что ни один узел не проходится более одного раза; непрерывность здесь означает, что в этой последовательности конец одной ветви является началом следующей.

Прямой путь есть путь, в котором каждая ветвь проходится только в направлении ее стрелки. В дальнейшем нам понадобятся только прямые пути. Два узла могут связывать и несколько прямых путей, отличающихся одной или несколькими ветвями.

Путевой множитель (путевое усиление) есть произведение всех множителей ветвей вдоль прямого пути. Каждый прямой путь имеет, вообще говоря, свой путевой множитель. Например, в графе на рис. 11.3.2б есть один прямой путь от узла 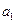(или, что то же самое, от узла 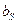) к узлу 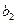с путевым множителем 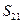, два прямых пути от узла 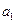к узлу 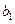с путевыми множителям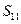и и 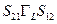соответственно, один прямой путь от узла 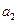к узлу 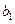с путевым множителем 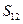и два прямых пути от узла 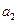к узлу 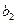с путевыми множителям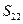и и 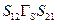соответственно.

Петля (прямая петля) есть прямой путь, который начинается и заканчивается на одном и том же узле. Один и тот же узел может состоять в нескольких петлях.

Петлевой множитель (петлевое усиление) есть произведение множителей ветвей вдоль петли. Например, в графе на рис. 11.3.2б есть две петли, начинающихся и заканчивающихся на узле 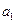с петлевыми множителям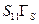и и 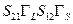соответственно, две петли, начинающихся и заканчивающихся на узле 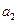с петлевыми множителям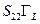и и 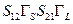соответственно.

Две или более петель называются непересекающимися (несоприкасающимися), если они не имеют не только общих ветвей, но даже общих узлов. Например, в графе на рис. 11.3.2б не пересекаются петля в левой части с петлевым множителем 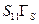и петля в правой части с петлевым множителем .

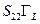Петля первого порядка – понятие тождественное понятию петля. Например, петли с петлевыми множителям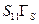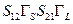и , и 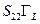суть петли первого порядка.

Петля второго порядка есть набор из двух непересекающихся петель первого порядка. Множитель петли второго порядка равен произведению множителей составляющих ее петель. Например, в графе на рис. 11.3.2б есть одна петля второго порядка, она объединяет две вышеупомянутых непересекающихся петли и имеет множитель .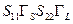

Петля 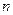-го порядка ( 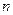=2, 3,…) есть набор из 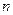непересекающихся петель первого порядка. Множитель петли 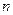-го порядка равен произведению множителей составляющих ее петель. Например, в графе на рис. 11.3.2б нет петель третьего и более высоких порядков.

На языке теории графов узел, ветвь, путь, петля могут пониматься как геометрические объекты или как величины (комплексные числа). Узел как величина есть значение соответствующей этому узлу переменной; ветвь, путь, петля как величины есть значения множителей этих объектов.

Переходя к технике отыскания частных решений потокового графа, сделаем три замечания.

1) Величина узла-стока (т. е. величина зависимой переменной, соответствующей этому узлу) равна сумме вкладов в этот узел от всех узлов-истоков, от которых имеется прямой путь к этому узлу. Это становится очевидным, если вспомнить, что потоковый граф есть графическое отображение соответствующей S - параметрической системы уравнений, в которой каждое уравнение представляет одну зависимую переменную как линейную комбинацию независимых переменных.

2) Вклад в зависимую переменную от одной независимой переменной, т. е. вклад в узел-сток от одного узла-истока находится по «правилу непересекающихся петель» Мэйсона (S. J. Mason), который предложил его в 50-е годы прошлого столетия и систематически его применял (см., например, [11.3, 11.4]). Строгий вывод этого правила на основе свойств определителей дан в [11.5].

3) Согласно этому правилу, вклад в зависимую переменную от одной независимой переменной равен произведению последней на некоторый множитель (переносная функция [11.9]), представляющий собой некоторое выражение от множителей ветвей графа. Обычно в качестве правила используют формулу для этого множителя, т. е. для отношения конкретной зависимой переменной к конкретной независимой переменной. Чтобы найти полное частное решение для конкретной зависимой переменной, находим вклад от каждой независимой переменной путем умножения переносной функции на величину последней и сложения всех таких произведений по независимым узлам, дающим вклад.

Формула для переносной функции от независимой переменной 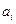к зависимой переменной 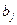имеет вид:

,

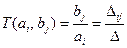(11.4.1)

где

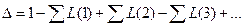,	(11.4.2)
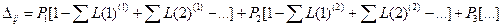,	(11.4.3)

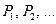– прямые пути для данной пары узлов;

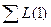– сумма всех петель первого порядка графа;

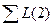– сумма всех петель второго порядка графа; …

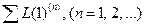– сумма петель первого порядка, не касающихся ни в одной точке прямого пути ;

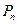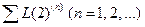– сумма петель второго порядка, не касающихся ни в одной точке прямого пути ; …

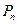Рис. 11.3.2. Схема и граф нагруженной двухпортовой цепи.

Заметим, что знаменатель 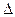формулы (11.4.1) одинаков для всех пар «независимый узел – зависимый узел» и зависит только от топологии графа. В графе на рис. 11.3.2б три петли первого порядка и их сумма

,

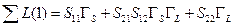(11.4.4)

одна петля второго порядка и

,

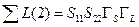(11.4.5)

нет петель третьего и более высоких порядков, в итоге

.

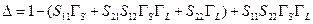(11.4.6)

Вычисляем 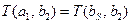. Для этой пары узлов имеется только один прямой путь: 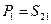и нет петель, не соприкасающихся с этим путем, поэтому

.

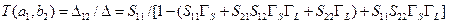(11.4.7)

Вычисляем 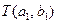. Для этой пары узлов имеется два прямых пут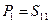и: и 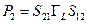. С путем 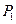не соприкасается только петля первого порядка 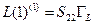; петель, не соприкасающихся с путем 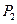нет. В итоге

,

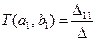(11.4.8)

где

.

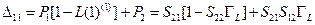(11.4.9)

Вычисляем 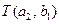. Для этой пары узлов имеется только один прямой путь: 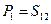и нет петель, не соприкасающихся с этим путем, поэтому

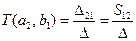
(11.4.10)

Вычисляем 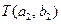. Для этой пары узлов имеется два прямых пут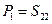и: и 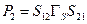. С путем 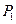не соприкасается только петля первого порядка 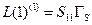; петель, не соприкасающихся с путем 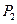, нет. В итоге

,

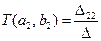(11.4.11)

где

.

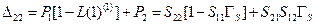(11.4.12)