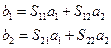Граф для линейной функции независимых переменных

Сигнальный граф и матричное представление линейной цепи. Потоковый граф

Решить сигнальный граф значит по заданным независимым переменным и весам ветвей найти некоторые или все зависимые переменные. При этом используются определенные правила, важнейшим из которых является рассмотренное ниже «правило непересекающихся петель» Мэйсона [11.3, 11.4]. Поскольку, как указано выше, сигнальный граф отображает линейные соотношения между процессами в реальной или эквивалентной цепи, то решение графа соответствует частичному или полному решению системы этих соотношений.

Узел, соответствующий независимой переменной, иногда называют истоком; такой узел имеет только исходящие ветви. Узел, имеющий только входящие ветви, тогда называется стоком, такой узел имеет только входящие ветви. Сигнальный граф может содержать также узлы третьего вида, имеющие как входящие, так и исходящие ветви; такой узел называется смешанным. Если переменная, соответствующая смешанному узлу, не подлежит определению при решении графа, то такой узел может быть устранен, т. е. построен новый, более простой эквивалентный граф. Эквивалентность означает [11.5], что соотношения между оставшимися переменными в новом графе точно такие же, как в первоначальном графе.

Поскольку сигнальный граф адекватен некоторой системе линейных уравнений для процессов цепи, возникает вопрос, в чем преимущества графического представления и решения графа в сравнении с непосредственным решением соответствующей системы уравнений. Действительно, любую систему линейных уравнений можно решить регулярными алгебраическими методами, например, методом исключения (методом Гаусса). Часто, однако, матрица системы уравнений имеет высокий порядок, что обусловливает большую громоздкость и малую обозримость решений, т. е. трудность интерпретации результатов. Преимущества графического подхода возникают, во-первых, из того, что на практике часто не требуется находить все зависимые переменные системы, а лишь некоторые из них (иногда даже одну переменную), т. е. полного решения системы не требуется. Во-вторых, обычно матрица системы имеет большое число нулей, что позволяет эффективно исключать узлы графа, причем само рассматривание графа позволяет выявить оптимальный порядок исключения узлов. В-третьих, решение с помощью графа обладает большей наглядностью и облегчает интерпретацию результатов решения.

Как известно [11.5], для любой заданной линейной системы (не обязательно радиотехнической) имеется множество способов выбора переменных и записей уравнений. С каждым набором уравнений связывается свой сигнальный граф, и таким образом данная линейная система может быть представлена с помощью множества различных сигнальных графов. Сказанное полностью относится к радиотехнической цепи, работающей в режиме переменных сигналов. Даже если ограничиться лишь эквивалентными радиотехническими цепями в виде линейных 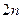-полюсников ( 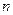-портовых цепей) и переменными только в виде токов и напряжений, то, как показано в главе 10, для одной 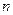-портовой цепи можно составить 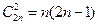различных систем линейных уравнений и, следовательно, различных сигнальных графов этой цепи с различными по физическому смыслу узлами. Как видим, число различных графов одной 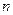-портовой цепи быстро нарастает с увеличением 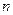: при 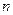=2 их 6, включая графы, соответствующие 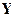, , 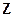, , 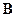, 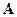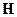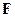-матричным представлениям, а при 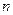=3 различных графов уже 15. Возникает вопрос: какое из представлений системой уравнений относительно токов и напряжений и соответствующих сигнальных графов наиболее удобно для анализа цепей, создаваемых при тестировании устройств СВЧ с помощью анализаторов цепей, для спектрального анализа и создаваемых при этом цепей и т.д., а также в измерениях с целью калибровки приборов СВЧ? Ответ состоит в том, что все варианты выбора переменных в виде токов и напряжений неудобны и неперспективны для достижения этих целей. По причинам, указанным в главе 10, наилучшим является выбор переменных не в виде токов и напряжений, а в виде нормированных падающих и отраженных волн на разъемах цепи (волн мощности). В этом случае система линейных уравнений (10.5.1), описывающая состояние линейной радиотехнической цепи в выбранном базисе плоскостей отсчета, имеет в качестве коэффициентов элементы матрицы 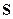рассеяния, т. е. реализует 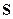-матричное представление. Этому представлению соответствует специальный вид сигнальных графов – сигнальный потоковый граф (далее прилагательное «сигнальный» опускаем).

В дополнение к высказанным выше аргументам в пользу применения вообще сигнальных графов, можно добавить соображения о полезности именно потоковых графов. Поскольку эти графы соответствуют представлению сигналов через падающие и отраженные волны, для интерпретации сигналов приходится учитывать отражения всех порядков от неоднородностей цепи. При этом уже цепь с более чем одной внутренней неоднородностью становится трудной для анализа путем бесконечного суммирования отраженных волн. На рис.11.2.1 [11.9] показаны лишь отражения невысокого порядка в системе «анализатор цепей – тестируемое устройство».

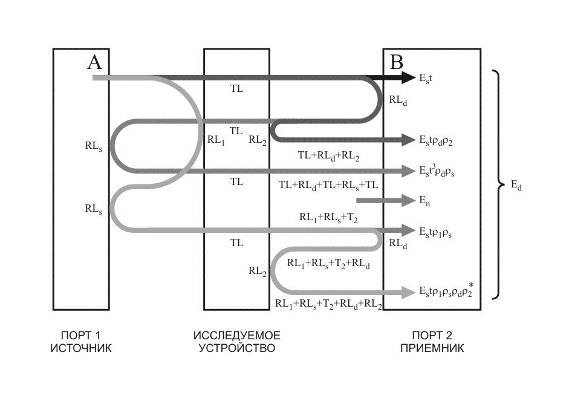
Отражения невысокого порядка в системе «анализатор – тестируемая цепь»

Хотя S-матричное представление формально решает эту проблему, проникновение в физический смысл соотношений в цепи уменьшается с увеличением ее сложности. Потоковый граф цепи, во-первых, помогает уяснить этот физический смысл, во-вторых, позволяет учесть отсутствующие на принципиальной схеме паразитные потоки, связанные с нежелательными отражениями и протечками, и в-третьих, позволяет проводить упрощения цепи путем хорошо обоснованных физически аппроксимаций и приближений.

Зафиксируем более точный и более узкий смысл, в котором далее будем использовать понятие потокового графа.

1) Потоковый граф будет пониматься как сигнальный граф, соответствующий 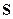-матричному описанию линейной эквивалентной цепи, состоящей из соединенных линиями передачи без потерь 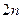-полюсников.

2) Переменными, которым соответствуют узлы потокового графа, будут комплексные амплитуды монохроматических волн мощности, нормированные соответствующим образом (см. главу 10).

3) Описываемая потоковым графом цепь может включать как распределенные, так и сосредоточенные элементы.

4) Потоковый граф может включать узлы и ветви, отражающие существование и распространение паразитных волн, обязанных протечкам, отражениям от паразитных элементов и другим явлениям, не учтенным электрической эквивалентной схемой цепи.

5) Каждому порту эквивалентной принципиальной схемы соответствует два узла графа: узел типа исток, из которого исходят направленные ветви, соответствующий входящей (падающей извне, например, от генератора) волне, при необходимости обозначается буквой 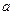с соответствующим индексом; узел типа сток, к которому подходят направленные ветви, соответствующий выходящей наружу (отраженной) волне, при необходимости обозначается буквой 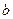с соответствующим индексом. Например, в случае двухпортовой цепи появляются узлы 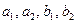и, возможно, узел 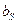, связанный с генератором. Разумеется, как и во всяком сигнальном графе, в потоковом графе могут быть смешанные (внутренние) узлы.

6) С каждой ветвью связан и указывается рядом с ней множитель ветви (в общем случае комплексный).

7) Ветви начинаются в узлах независимых переменных и заканчиваются на узлах зависимых переменных (зависимость и независимость устанавливаются соответствующими уравнениями). На каждой ветви указывается стрелкой направление потока и числом или буквой – множитель.

8) Если поток от узла независимой переменной к узлу зависимой переменной проходит без изменения, то на связывающей их ветви указывается множитель 1.

9) Величина каждой зависимой переменной определяется множителями и независимыми переменными, связанными с ветвями от соответствующих узлов.

10) Хотя сказанное выше о структуре сигнального графа, естественно, остается в силе и для потокового графа, в построении, виде и интерпретации последнего имеется своя специфика, диктуемая, в основном, удобством работы с ним. Эта специфика будет проиллюстрирована примерами.

Декларированное выше удобство потоковых графов для анализа процессов измерения параметров устройств СВЧ с помощью анализаторов цепей было осознано давно и объясняется, во-первых, тем, что описываемая этими графами цепь может включать как распределенные, так и сосредоточенные элементы, во-вторых, простотой учета с помощью этих графов паразитных волн, что необходимо в рассмотрении систематических и случайных ошибок измерения и методов калибровки анализаторов цепей. Другим объектом стандартного применения потоковых графов, восходящего к работам [11.3, 11.4], являются цепи с обратными связями.

Построение потокового графа

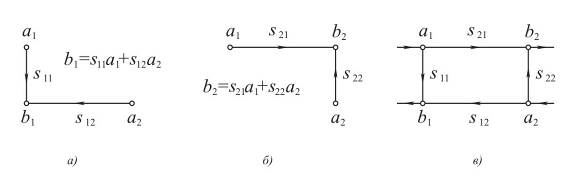
Рис. 11.3.1, 11.3.2 иллюстрируют построение потоковых графов по уравнениям в S-параметрах или по принципиальным схемам в рамках ненагруженного и нагруженного четырехполюсников. Рис. 11.3.1 поясняет составление графа ненагруженного четырехполюсника, соответствующего S-параметрической системе уравнений (11.3.1)