Координата в линии передачи

Можно выразить напряжение и ток в линии через текущий коэффициент отражения:

,

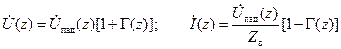(12.1.2)

где 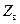– волновое сопротивление линии. Деля напряжение в сечении 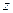на ток в том же сечении, получаем входное сопротивление как функцию координаты :

.

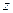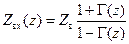(12.1.3)

Удобно пользоваться нормированным входным сопротивлением:

,

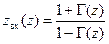(12.1.4)

и наоборот:

.

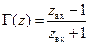(12.1.5)

В силу периодичности 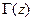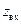также периодично с тем же периодом .

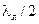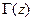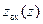С общематематической точки зрения уравнения (12.1.4), (12.1.5) представляют собой преобразования Мёбиуса, связывающие функции и ; с позиций теории функций комплексного переменного это частный случай дробно-линейных преобразований. Подобные соотношения часто встречаются в прикладной электродинамике и теории цепей. Круговая диаграмма как раз и предназначена для наглядного выполнения и интерпретации этих преобразований. Функци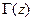и и 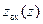параметрически зависят от частоты.

Векторная диаграмма падающей и отраженной волн

Идея КД состоит в том, чтобы текущий коэффициент отражения 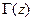выражался своими модулем и углом в полярной диаграмме на комплексной плоскости, а нормированное сопротивление 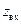– в декартовой системе координат на той же плоскости. Так как 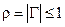, то на конкретной частоте и в конкретном сечен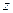ии линии 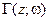будет выражен точкой внутри круга единичного радиуса, а на совокупности частот в некоторой полосе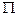 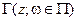отобразится некоторой траекторией внутри этого круга. С другой стороны, как следует из (12.1.1), на данной частоте 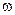с ростом 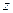(т. е. по мере приближения к генератору) точка 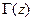движется по окружности радиуса 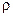в направлении по часовой стрелке с текущим углом 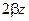. 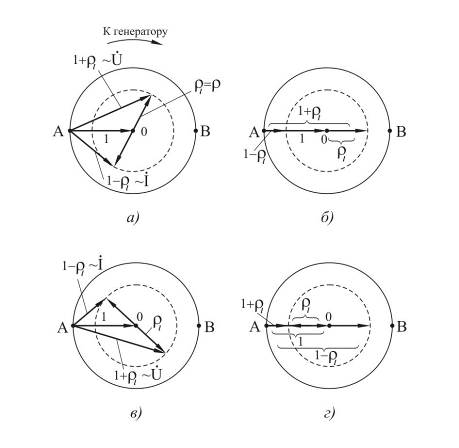Прежде чем обратиться к собственно КД, следуя [12.3], рассмотрим векторную диаграмму полных напряжения и тока в линии в зависимости от 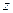(рис.12.2.1).