Генераторы, нормализованные волны и полные токи и напряжения двухпортовой цепи.

Перейдем теперь к двухпортовой цепи (четырехполюснику). В общем случае она возбуждается с обоих портов (рис. 10.9.3), по аналогии со случаем однопортовой цепи можно записать:

,

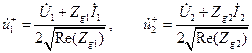и основная система в терминах параметров рассеяния повторяет уравнения:

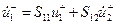,	(10.6.4)
.	(10.6.5)

Наконец, в общем случае 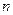-портовой цепи падающие нормализованные волны:

,

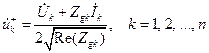и основная система в терминах параметров рассеяния повторяет уравнения:

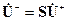,	(10.5.1)
или в расписанном виде:
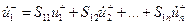
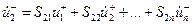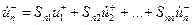
…………………………….. ……………………………..	(10.5.2)

Изменение опорных плоскостей

Как отмечено выше, комплексные амплитуды нормализованных волн относятся к опорным плоскостям. Следовательно, и связывающие эти волны параметры рассеяния также относятся к опорным плоскостям; при изменении положения хотя бы одной опорной плоскости параметры рассеяния, вообще говоря, изменяются. Выявим закономерность этих изменений. Пусть характеризуемое параметрами рассеяния устройство является сочленением 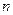однородных линий передачи без потерь с коэффициентами фазы 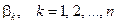; опорные плоскости изменили свое положение на 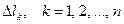, не обязательно все отличные от нуля (положительное направление сдвига опорной плоскости – от сочленения). Из (10.6.2), (10.6.3) следует, что новое значение 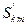параметра рассеяния выражается через старое значение как

.

(10.10.1)

В соответствии с этой системой соотношений, новая матрица рассеяния выражается через «старую» 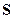как

,

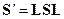где 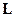– диагональная матрица порядка 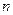, диагональные элементы которой имеют значения 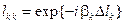. В рассматриваемом частном случае линий без потерь изменение положения опорных плоскостей влияет только на аргументы (фазы) параметров рассеяния, оставляя неизменными их модули (это полезное свойство не выполняется для классических характеристических матриц: при сдвиге опорных плоскостей элементы этих матриц меняются как по фазе, так и по амплитуде). В общем случае линий передачи с потерями приведенные соотношения остаются в силе, если заменить в них 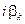на постоянные распространения 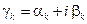, где 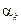– коэффициенты затухания линий. Из (10.10.1) следует, что любой комплексный параметр рассеяния можно сделать действительным, изменив определенным образом положение соответствующей опорной плоскости. Так как всего опорных плоскостей 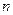, то максимальное число таких превращений также равно 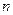, в то время как всего параметров рассеяния .

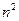Математические свойства матриц рассеяния

В зависимости от внутреннего устройства многополюсника его матрица рассеяния имеет те или иные математические свойства [10.9]. Чем более подробно известны внутренние свойства многополюсника, тем больше, в принципе, свойств можно обнаружить у его матрицы рассеяния. Однако существуют важные классы устройств, которым соответствуют довольно общие свойства матриц рассеяния, важные в приложениях. Приведем эти свойства без вывода. Как показано выше, матрица 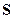рассеяния существует для любого пассивного линейного 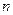-портового устройства, имеет размер ( 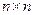), ее элементы в общем случае комплексны и безразмерны.

1) Устройство СВЧ, в котором использованы только изотропные материалы, является взаимным. Матрица 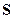рассеяния взаимного устройства симметрична, т. е. , или 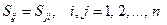(значок « 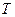» означает транспонирование). Справедливо и обратное: если матрица рассеяния устройства симметрична, то оно взаимно.

2) Если многополюсник не имеет потерь, он называется недиссипативным. Матрица рассеяния недиссипативного устройства унитарна, т. е.

,

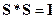где 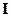– единичная матрица порядка 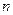, «звездочка» означает эрмитово сопряжение, т. е. последовательные транспонирование и комплексное сопряжение элементов. Справедливо и обратное: если матрица рассеяния устройства унитарна, то оно недиссипативно. Из теории матриц известно, что столбцы (а также строки) унитарной матрицы ортонормированны:

,

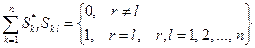т. е. модуль вектора-столбца (вектора-строки) унитарной матрицы равен единице:

,

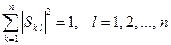а скалярное произведение двух разных векторов-столбцов (векторов-строк) равно нулю.

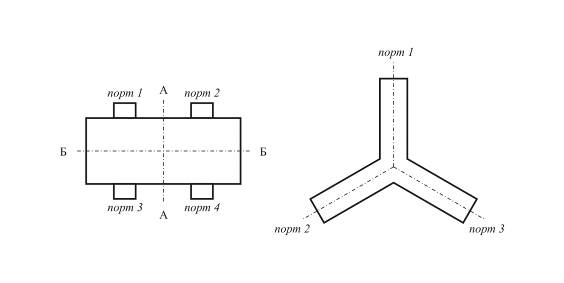
3) Устройство СВЧ называется симметричным, если оно не изменяется (инвариантно) при преобразовании симметрии, т. е. повороте устройства вокруг некоторой оси на какой-то угол, зеркальном отображении относительно какой-либо плоскости и т. п. Существуют различные типы симметрии, им соответствуют различные преобразования симметрии. Любое преобразование симметрии есть перенумерация портов без изменения самого устройства. На рис. 10.11.1 приведены простые примеры симметричных многополюсников: четырехпортовое устройство с зеркальной симметрией относительно плоскостей А-А и Б-Б (рис. 10.11.1(а)) (устройство не меняется при замене номеров портов 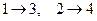и наоборот, и (или) номеров портов 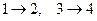и наоборот); симметричный Y-тройник с поворотной симметрией на 120⁰ (рис. 10.11.1(б)) (устройство не меняется при замене номеров портов 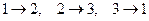и наоборот).

(слева, справа))

Слева: четырехпортовое устройство с зеркальной симметрией относительно плоскостей А-А и Б-Б. Справа: симметричный тройник с поворотной симметрией на 120⁰

Общий метод учета симметрии данного устройства и формулировки следующих из нее соотношений элементов матрицы рассеяния таков:

А) Для каждой отдельной симметрии составляется матрица симметрии. Это квадратная матрица того же порядка , что и матрица 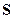. В каждом столбце (и в каждой строке) имеется один элемент, равный 1, остальные равны нулю (поэтому 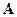унитарна); для единичного элемента, стоящего на пересечении 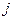-го столбца и 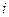-ой строки, 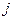– номер порта до преобразования симметрии, 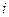– номер того же порта после преобразования симметрии. Например, для симметричного тройника (рис. 10.11.1 (справа)) матрица симметрии имеет вид:

;

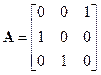четырехпортовое устройство с двумя плоскостями симметрии (рис. 10.11.1 (слева)) имеет две симметрии: относительно плоскости А-А и относительно плоскости Б-Б, им соответствуют матрицы симметрии:

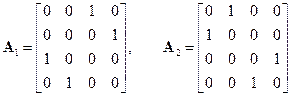
(заметим, что 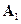симметрична относительно главной диагонали, а 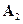– относительно побочной диагонали). Обратное преобразование симметрии описывается матрицей симметрии 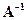, а поскольку 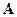унитарна, то = .

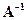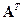Б) Следующие из симметрии устройства свойства элементов матрицы 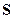получаются из системы равенств (одного матричного равенства):

,

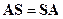означающей, что матрицы 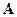и 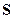коммутируют. Если у устройства несколько симметрий, которым соответствует несколько матриц симметрии, то 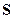коммутирует с каждой из них. Например, для приведенного на рис. 10.11.1 (слева) устройства одновременно справедливы равенства

, .

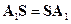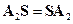Несмотря на наличие общего метода учета симметрий, часто следующие из симметрии устройства свойства элементов матрицы 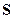находят непосредственно, глядя на рисунок и не прибегая к построению матрицы симметрии.

Главное значение рассмотренных общих математические свойства матриц рассеяния состоит в том, что использование этих свойств (если к этому есть основания: взаимность, отсутствие потерь и (или) симметрии) позволяет уменьшить число независимых элементов матрицы рассеяния и, тем самым, число параметров рассеяния, которые необходимо непосредственно измерять.