Диаграмма Вольперта-Смита с укрупненными шагами.

Чертеж круговой диаграммы показан на рис. 12.3.3. Для удобства изучения шаги по 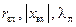взяты более крупными, чем обычно берут в рабочих диаграммах. Как видим, диаграмма расположена внутри круга единичного радиуса, оси 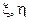опущены, нанесены (с определенным шагом) окружности постоянной активной части 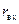входного сопротивления и попадающие в диаграмму части окружностей постоянной реактивной части 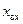входного сопротивления, по границе круга единичного радиуса в долях 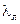нанесен фазовый угол 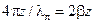текущего коэффициента отражения (индекс «л» в обозначении длины волны опущен), показаны направления движения по окружности «к генератору» и «к нагрузке». Надпись «Активное сопротивление» напоминает, что горизонтальная ось диаграммы есть вырожденная в прямую окружность постоянной 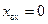, т. е. геометрическое место точек чисто активных входных сопротивлений. Надписи «Индуктивное сопротивление» и «Емкостное сопротивление» напоминают, что окружности постоянных положительных 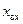расположены в верхней полуплоскости, постоянных отрицательных 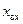– в нижней полуплоскости 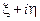. Диаграмма, рассчитанная на многократное применение, иногда изготавливается как отдельное графическое устройство, в котором, кроме собственно круговой диаграммы имеется прозрачный вращающийся вокруг центра диаграммы движок с нанесенной на нем шкалой КСВ или модуля 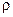коэффициента отражения. Если диаграмма не снабжена движком, то шкалы КСВ и 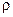показаны на горизонтальной прямой, расположенной под диаграммой.

Отметим, что нанесенная на диаграмме координатная сетка в виде двух семейств окружностей позволяет отобразить на диаграмме все возможные значения полного нормированного сопротивления 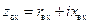. Последнее отображается в виде точки пересечения двух окружностей: одна есть окружность постоянного заданного 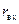, другая – окружность постоянного заданного 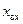. Наоборот, каждая точка диаграммы соответствует некоторому 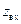. В то же время, каждая точка диаграммы соответствует некоторому текущему комплексному коэффициенту отражения 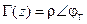: модуль 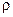коэффициента отражения равен радиусу окружности с центром 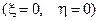, на которой лежит точка (т. е. расстоянию от точки до центра диаграммы); 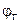равен углу вектора, проведенного в точку из центра диаграммы. 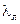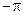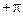Иногда на внешней окружности диаграммы, кроме шкалы в долях , наносится азимутальная шкала в радианах (от до ) или в градусах (от -180⁰ до +180⁰), позволяющая определить 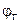. В этом случае для отсчета 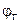следует провести прямую из центра диаграммы через данную точку до пересечения с азимутальной шкалой, и по ней отсчитать .

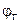Заметим также, что изображающая точка 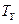нормированной входной проводимости 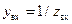симметрична изображающей точке 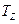нормированного входного сопротивления 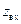относительно центра диаграммы. Действительно, поскольку 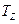суть конец вектора 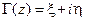и

,

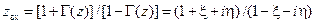то конец вектора 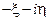суть изображающая точка комплекса

.

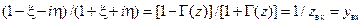Примеры применения круговой диаграммы

А) Определение модуля коэффициента отражения и КСВ по заданному входному сопротивлению. Пусть задано входное сопротивление 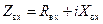и активное волновое сопротивление 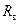. Делим 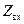на 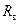, получая нормированное входное сопротивлени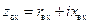е , где 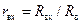, 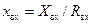. Выделяем окружности постоянного 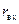и постоянного 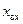, на их пересечении находится точка 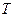. Модуль 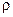коэффициента отражения находится как расстояние точки 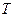от центра диаграммы в выбранном масштабе; его и 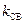можно определить по шкале на движке или по шкале, нанесенной на поддиаграммной прямой.

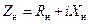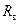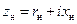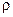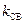Б) Определение модуля и фазы коэффициента отражения и КСВ по заданному сопротивлению нагрузки. Пусть задано сопротивление нагрузки и волновое сопротивление . Находим нормированное сопротивление нагрузки , далее действуем как в п. А). Кроме и , можно определить 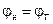, беря отсчет по азимутальной шкале на внешней окружности диаграммы. Если необходимо знать действительную и мнимую части коэффициента отражения 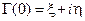, их отсчет можно взять на осях декартовой системы .

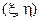В) Определение входного сопротивления нагруженной линии заданной длины. Пусть заданы сопротивление нагрузки 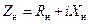, волновое сопротивление 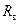и длина линии 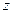. Как в п. Б), находим нормированное сопротивление нагрузки 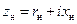, изображающую 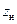точку 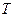на диаграмме, вектор 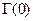с концом в точке 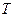. Используя азимутальную шкалу на внешней окружности диаграммы, поворачиваем вектор 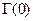по часовой стрелке на 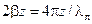рад и выделяем окружности постоянного 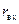и постоянного 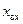, тем самым находя .

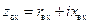Г) Определение расстояний от нагрузки до ближайших пучности и узла напряжения. Пусть заданы 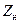и 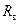. Найдя точку, изображающую 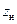, поворачиваем вектор 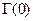с концом в этой точке по часовой стрелке до совпадения с отрезком 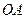(угол поворота 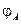) и до совпадения с отрезком 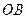(угол поворота 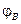). Расстояние от нагрузки до ближайшего узла напряжения равно 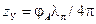, а до ближайшей пучности напряжения – .

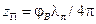Д) Определение сопротивления нагрузки с помощью измерительной линии. Пусть с помощью измерительной линии измерено распределение амплитуды стоячей волны напряжения вдоль линии, в результате чего известны напряжение в пучности 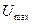, напряжение в узле 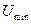, вид ближайшего к нагрузке экстремума (пучность или узел) и расстояние 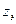от него до нагрузки. Вычисляем модуль 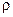коэффициента отражения по формуле:

,

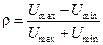тем самым выделяем окружность радиуса 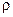с центром в начале (0, 0) диаграммы. Находим изображающую точку 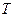сдвигом по этой окружности против часовой стрелки на угол 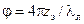: от пересечения окружности с отрезком 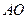, если ближайший к нагрузке экстремум напряжения – узел; от пересечения окружности с отрезком 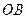, если ближайший к нагрузке экстремум напряжения – пучность. Активную и реактивную части 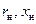нормированного сопротивления нагрузки 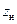находим по пересекающимся в т. 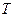окружностям постоянного 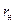и постоянного .

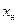Е) Согласование с помощью сосредоточенной реактивности. Пусть линия передачи нагружена на сопротивление 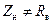, т. е. не согласована. Одним из способов согласования линии является последовательное или параллельное включение в нее сосредоточенной реактивности на некотором расстоянии от нагрузки. С помощью диаграммы необходимо определить как алгебраическую величину 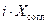включаемой реактивности, так и расстояние 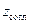от места ее включения до нагрузки. Для решения задачи важно заметить, что в результате согласования во всех сечениях слева от включенной реактивности нормированное входное сопротивление должно равняться 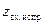=1. Решение таково: отмечаем изображающую точку 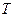нормированного сопротивления нагрузки 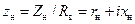(см. пп. А), Б)). Двигаясь по часовой стрелке по окружности постоянного 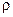, проходящей через 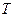, находим две точки пересечения этой окружности с окружностью постоянного 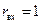. Одна точка пересечения, точка 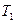, соответствующая повороту 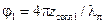, находится в верхней полуплоскости диаграммы; другая, точка 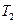, соответствующая повороту 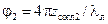, находится в нижней полуплоскости диаграммы. Выделяем окружности постоянной реактивности входного сопротивления, проходящие через тт. 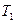, , 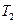и тем самым находим соответствующие нормированные реактивности 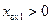(индуктивная) и 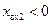(емкостная), соответствующие расстояниям от нагрузк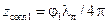и и 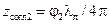. Для согласования нужно или компенсировать одну из этих реактивностей, или другую, т. е. или включить последовательно к линии в сечении 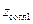реактивность 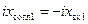(емкость), или в сечении 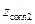реактивность 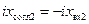(индуктивность). Заметим, что при выполнении одной компенсации другая происходит автоматически. Напомним также, что поскольку величины реактивностей зависят от частоты колебаний, выполненное согласование действительно только на одной частоте (той самой, на которой действительно использованное значение ).

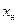Аналогичным образом, можно выполнить согласование линии с помощью параллельного включения (шунтирующей) реактивности в некотором сечении линии, для этого нужно использовать не входные сопротивления, а входные проводимости.