Диаграмма Айнса-Стретта.

Для практических целей главный интерес представляет определение границ между областями устойчивых и неустойчивых решений. Ответ на этот вопрос дает диаграмма Айнса-Сретта (рис.4.5). Она может быть построена для уравнения Мейснера в координатах 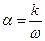, 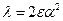с использованием численных методов интегрирования. Ею пользуются при отсутствии программного обеспечения, позволяющего ответить на вопрос об устойчивости движения.

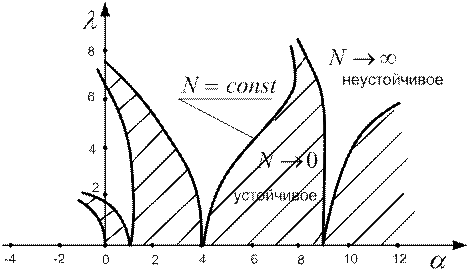
Рис.4.5

На диаграмме заштрихованные области соответствуют устойчивому состоянию системы 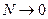. Не заштрихованные области соответствуют неустойчивому состоянию системы, когда колебания неограниченно возрастают 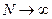. Иногда их называют параметрическим резонансом. Сплошные линии на диаграмме соответствуют периодическим режимам .

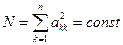Уравнение Матье.

Это однородное дифференциальное уравнение.

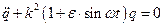. (4.6)

Введем обозначения 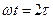; ; 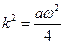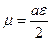, тогда уравнение Матье запишется в безразмерном виде

.

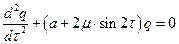Исследованиями этого уравнения занимались Дж. Релей и Айнс. Решение записывается в специальных функциях, которые получили название функции Матье. Мы будем строить решение с помощью матрицы переноса, так же как это осуществлялось для уравнения Мейснера. Построим матрицу переноса для уравнения Матье.

1. Интегрируем численно уравнение

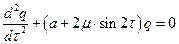
на интервале 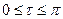( 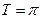) при начальных условиях 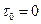: 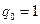, 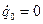. В результате численно находим компоненты первого столбца матрицы переноса , .

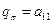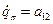2. Интегрируем то же уравнение на интервале 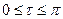при начальных условиях 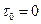: 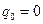, 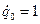. В результате находим компоненты второго столбца матрицы переноса , .

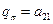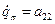3. После повторения этой процедуры строим матрицу переноса для момента кратного любому количеству периодов 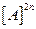. После чего вычисляем ее норму 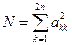. По найденному значению нормы можно судить о характере колебательного движения системы. При этом возможны три случая:

1. 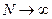- неустойчивое движение;

2. 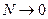- устойчивое движение;

3. 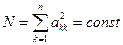- граница раздела между областями устойчивого и неустойчивого движения. Физически это соответствует случаю установившегося периодического движения. При этом амплитуда колебаний не возрастает с течением времени, поэтому значение обобщенных координат по истечении периода может быть вычислено по формуле

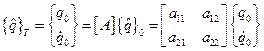или ,

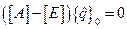где 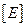- единичная матрица. Следовательно, в силу однородности уравнения для определения границ устойчивого движения может быть использовано условие 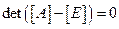. Точно так же с помощью матрицы переноса можно построить алгоритм проверки устойчивости для уравнения Хилла.

Как и в предыдущем случае для данного колебательного процесса может быть построена диаграмма Айнса-Стретта (см. рис.4.5).

Замечание. При численном интегрировании уравнения Матье на интервале 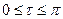нельзя использовать процедуру автоматического выбора шага, иначе в области неустойчивости точность расчета может быть не достигнута, вследствие чего может возникнуть сбой вычислительной процедуры.

ПРИМЕР. 1. Найти при каком сочетании параметров 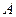, , 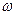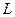и 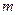вертикальное положение обращенного маятника будет устойчивым, если задан закон вертикального перемещения шарнирной опоры маятника .

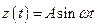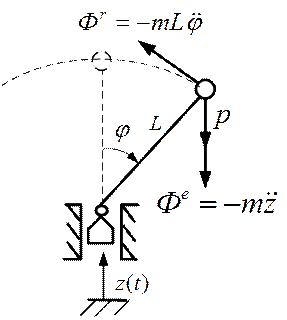
Рис.4.6

РЕШЕНИЕ. Для описания относительного колебательного движения будем использовать обобщенную координату 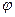. Для составления уравнения движения воспользуемся принципом Даламбера. Составим уравнение моментов относительно центра вращения:

.

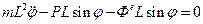Учитывая, что сила инерции переносного движения равна 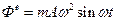, и, ограничиваясь малыми отклонениями маятника от вертикали 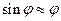, найдем

.

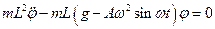И окончательно

.

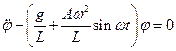Воспользуемся обозначениями 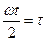; ; 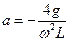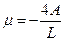, тогда уравнение движения примет вид

.

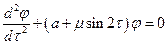С помощью построения матрицы переноса можно показать, что движение обращенного маятника будет устойчивым, если выполняется условие

.

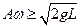Это означает, что движение будет устойчивым, если амплитудное значение скорости движения основания (точки подвеса) будет больше или равно той скорости, которую приобрел бы шарик, падая с высоты 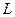без начальной скорости.

Впервые возможность стабилизации маятника в перевернутом положении за счет вертикальных колебаний точки подвеса установил А. Стефенсон в 1907 году. В заключении заметим, что все вышесказанное справедливо для линейного дифференциального уравнения. С ростом амплитуды изменения параметра начинает сказываться роль нелинейных факторов, которые нами не принимались в расчет. Вопрос о существовании устойчивых периодических решений в таком случае требует особого рассмотрения с привлечением теории нелинейных колебаний.