II. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ
ПОСТАНОВКА ЗАДАЧИ
Удельным зарядом 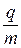 называют отношение заряда
называют отношение заряда 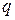 частицы к её массе
частицы к её массе 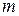 . Заряд и масса частицы являются её важнейшими характеристиками. Благодаря наличию заряда, частица испытывает действие сил со стороны электрического и магнитного полей. Масса является мерой её инерционных свойств. Таким образом, заряд и масса определяют вектор ускорения частицы, приобретаемого в заданных электрическом и магнитном полях, т.е. характер её движения.
. Заряд и масса частицы являются её важнейшими характеристиками. Благодаря наличию заряда, частица испытывает действие сил со стороны электрического и магнитного полей. Масса является мерой её инерционных свойств. Таким образом, заряд и масса определяют вектор ускорения частицы, приобретаемого в заданных электрическом и магнитном полях, т.е. характер её движения.
Заряд не зависит от скорости движения и является инвариантом во всех инерциальных системах отсчёта. Масса частицы зависит от скорости её движения. Согласно теории относительности, при скоростях движения частицы близких к скорости света, масса частицы равна
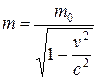
где 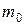 - масса покоя,
- масса покоя, 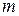 - масса частицы, движущейся со скоростью
- масса частицы, движущейся со скоростью 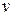 ,
, 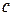 - скорость света в вакууме.
- скорость света в вакууме.
Поэтому удельный заряд 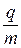 также будет зависеть от скорости движения частиц
также будет зависеть от скорости движения частиц 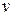 :
:
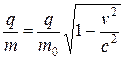 .
.
В наших опытах частицы имеют скорости 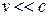 , поэтому релятивистским эффектом вполне можно пренебречь и считать удельный заряд, не зависящим от скорости движения частицы.
, поэтому релятивистским эффектом вполне можно пренебречь и считать удельный заряд, не зависящим от скорости движения частицы.
Определение удельного заряда имеет большое практическое значение, в частности, для идентификации и изучения свойств элементарных частиц и изотопов.
В данной работе определяется удельный заряд 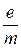 электрона на основе исследования его движения в скрещенных электрическом и магнитном полях.
электрона на основе исследования его движения в скрещенных электрическом и магнитном полях.
II. ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В ЭЛЕКТРИЧЕСКОМ И МАГНИТНОМ ПОЛЯХ
На движущиеся заряженные частицы могут действовать электрическое и магнитное поля. В общем случае при наличии и электрического и магнитного полей результирующая сила, действующая на частицу, определяется по принципу суперпозиции полей
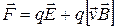 , (1)
, (1)
где 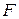 - результирующая сила, сила Лоренца,
- результирующая сила, сила Лоренца, 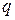 - заряд частицы;
- заряд частицы; 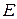 - напряжённость электрического поля;
- напряжённость электрического поля; 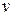 - скорость частицы;
- скорость частицы; 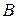 - индукция магнитного поля.
- индукция магнитного поля.
 Первое слагаемое
Первое слагаемое 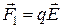 определяет воздействие электрической составляющей, второе
определяет воздействие электрической составляющей, второе 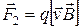 - воздействие магнитной составляющей электромагнитного поля. Часто именно
- воздействие магнитной составляющей электромагнитного поля. Часто именно 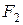 называется силой Лоренца.
называется силой Лоренца.
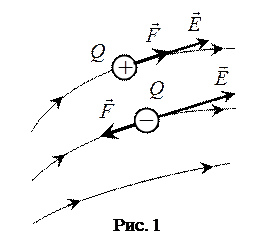
Сила 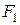 зависит от величины и знака движущегося заряда и напряжённости электрического поля (рис. 1). Для положительных зарядов действие силы совпадает с направлением напряженности
зависит от величины и знака движущегося заряда и напряжённости электрического поля (рис. 1). Для положительных зарядов действие силы совпадает с направлением напряженности 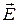 .
.
Если заряженная частица движется вдоль силовой линии электрического поля, то электрическое поле влияет на величину скорости движения и, следовательно, изменяет её кинетическую энергию.
Если скорость направлена под углом к направлению напряженности, то поле изменяет и величину, и направление скорости  . В этом случае изменяется не только энергия частицы, но и наблюдается искривление траектории движения частицы .
. В этом случае изменяется не только энергия частицы, но и наблюдается искривление траектории движения частицы .
 Сила
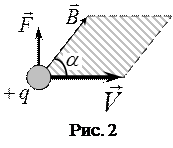
Сила  со стороны магнитного поля
со стороны магнитного поля
зависит от знака и величины заряда час-
тицы, а также от направления и величины ско-
рости движения 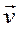 и от величины и направле-
и от величины и направле-
ния магнитного поля 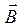 (рисю2). Направле-
(рисю2). Направле-
ние силы Лоренца находят по правилу левой
руки: четыре пальца левой руки располагают по направлению скорости движения положительно заряженной частицы 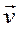 , при этом силовые линии магнитного поля
, при этом силовые линии магнитного поля 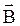 входят в открытую ладонь, тогда как большой отогнутый палец показывает направление действия силы
входят в открытую ладонь, тогда как большой отогнутый палец показывает направление действия силы 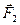 Величина силы определяется как модуль векторного произведения векторов
Величина силы определяется как модуль векторного произведения векторов 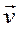 и
и 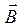 .
.
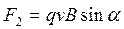 , (2)
, (2)
где 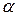 - угол между направлением движения частицы
- угол между направлением движения частицы 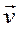 и вектором
и вектором 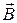 .
.
Из уравнения (1) следует, что сила 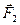 всегда перпендикулярна к скорости движения частицы
всегда перпендикулярна к скорости движения частицы 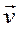 , поэтому скорость изменяется лишь по направлению, но не по величине. Следовательно, кинетическая энергия частицы в магнитном поле остается постоянной, а импульс частицы
, поэтому скорость изменяется лишь по направлению, но не по величине. Следовательно, кинетическая энергия частицы в магнитном поле остается постоянной, а импульс частицы 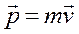 изменяется лишь по направлению. Эта сила
изменяется лишь по направлению. Эта сила 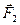 не совершает работы, а вызывает лишь искривление траектории движения.
не совершает работы, а вызывает лишь искривление траектории движения.
В зависимости от угла 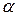 между направлением скорости
между направлением скорости 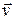 и вектором индукции
и вектором индукции 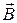 возможны
возможны 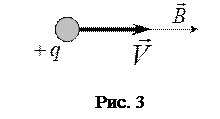 следующие
следующие  траектории движения положительных зарядов.
траектории движения положительных зарядов.
а) Заряженная частица движется вдоль силовой линии. Скорость 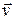 совпадает с вектором
совпадает с вектором 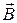 , т.е.
, т.е.  (рис. 3). Как видно из уравнения (2),
(рис. 3). Как видно из уравнения (2),  , т.е. магнитное поле не действует на такие частицы.
, т.е. магнитное поле не действует на такие частицы.
б) Заряженная частица движется перпендикуляр-
но к силовым линиям. Скорость движе  ния
ния 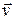 перпенди-
перпенди-
кулярна к вектору 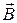 , т.е.
, т.е.  (рис. 4).
(рис. 4).
Из формулы (1) следует, что сила Лоренца 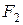 всег-
всег-
да направлена перпендикулярно к скорости движения
частицы и, поэтому, может сообщать ей только центро-
стремительное ускорение и модуль скорости в процессе
движения меняться не будет.
Исходя из второго закона Ньютона, данная сила 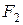
вызывает ускорение 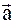 , совпадающее с силой по направлению.
, совпадающее с силой по направлению.
С учётом формулы (1) уравнение второго закона Ньютона запишется:
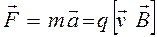 . (3)
. (3)
Из рис.4 следует, частица, влетающая в однородное магнитное поле перпендикулярно к силовым линия, будет двигаться по окружности радиусом 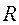 с постоянным периодом обращения
с постоянным периодом обращения 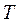 .
.
Для однородного магнитного поля ( 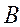 = const) уравнение (3) с учётом формулы (2) примет вид:
= const) уравнение (3) с учётом формулы (2) примет вид: 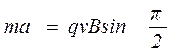 , (4)
, (4)
где 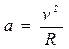 - центростремительное ускорение.
- центростремительное ускорение.
Тогда формула (4) будет выглядеть следующим образом:
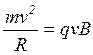 . (5)
. (5)
Радиус окружности, по которой движется частица, определяют исходя формулы (5) 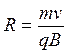 . (6)
. (6)
Период обращения заряда по траектории находят по определению с учетом формулы (6):
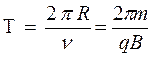 (7)
(7)
где  - удельный заряд частицы.
- удельный заряд частицы.
Из формулы (7) следует, что период обращения частицы по окружности зависит только от удельного заряда частицы 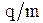 и индукции магнитного поля
и индукции магнитного поля 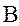 .
.
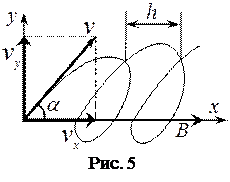
 г) Частица движется в магнитном поле под углом
г) Частица движется в магнитном поле под углом 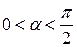 (рис. 5). Такое движение может быть рассмотрено как два движения с составляющими скорости
(рис. 5). Такое движение может быть рассмотрено как два движения с составляющими скорости 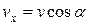 и
и 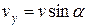 . Движение вдоль оси
. Движение вдоль оси 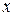 соответствует рассмотренной ситуации (а), а движение вдоль оси
соответствует рассмотренной ситуации (а), а движение вдоль оси 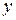 - ситуации (б). В результате частица будет двигаться по сложной кривой - винтовой линии.
- ситуации (б). В результате частица будет двигаться по сложной кривой - винтовой линии.
Эта линия характеризуется радиусом 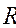 и шагом h винтовой линии (шаг винтовой линии h - расстояние между соседними витками).
и шагом h винтовой линии (шаг винтовой линии h - расстояние между соседними витками).
Исходя из уравнения (6) и скорости движения 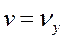 , радиус винтовой линии
, радиус винтовой линии  определяют по формуле:
определяют по формуле:
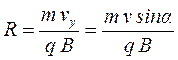 (8)
(8)
Шаг винтовой линии определяют по формуле :
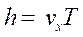 . (9)
. (9)
С учётом формулы (7) и скорости  , формула (9) примет следующий вид:
, формула (9) примет следующий вид:
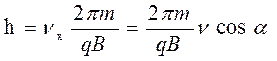 . (10)
. (10)
Дата добавления: 2016-03-10; просмотров: 19815;
