Главные (нормальные) координаты.
Изменение каждой обобщенной координаты во времени представляет собой наложение двух простых гармонических колебаний с произвольными амплитудами и фазами, определяемыми из начальных условий, но имеющими определенные частоты и коэффициенты форм, которые зависят только от инерционно-жесткостных характеристик. Изменение координат в общем случае будет негармоническим. Возникает естественный вопрос: нельзя ли выбрать обобщенные координаты 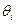 так, чтобы каждая из них изменялась по гармоническому закону
так, чтобы каждая из них изменялась по гармоническому закону
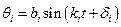
Формулы (3.6) и (3.7) можно рассматривать как формулы линейного преобразования координат 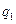 и
и 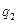 в координаты
в координаты 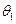 и
и 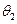
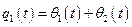 ;
; 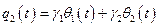 (3.19)
(3.19)
Воспользуемся представлением обобщенных координат в форме матрицы - столбца
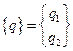 и
и 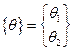 ,
,
Тогда линейное преобразование (3.19) можно записать в матричной форме
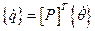 ,
,
где 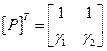 -транспонированная матрица матрицы линейных преобразований
-транспонированная матрица матрицы линейных преобразований 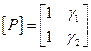 , строки матрицы
, строки матрицы 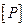 представляют собой формы собственных колебаний. Справедливо соотношение
представляют собой формы собственных колебаний. Справедливо соотношение
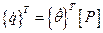
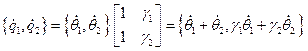
В старых обобщенных координатах кинетическая и потенциальная энергии записываются так
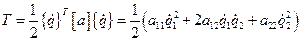 ,
,
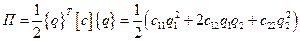 .
.
Кинетическая и потенциальная энергии, записанные в новых координатах, содержат лишь квадраты обобщенных скоростей и координат
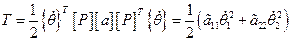 ,
,
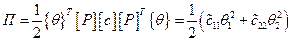 .
.
Введем новые определения для обобщенных масс и жесткостей
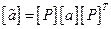 - новые обобщенные массы,
- новые обобщенные массы,
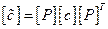 - новые обобщенные жесткости.
- новые обобщенные жесткости.
Кинетическая и потенциальная энергии в новых координатах запишутся в виде
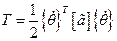 ,
, 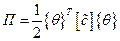 .
.
Установленная связь между матрицами обобщенных коэффициентов инерции и жесткости
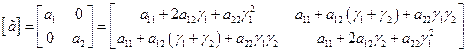 ,
,
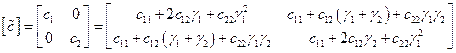 ,
,
позволяет получить очень важные формулы для вычисления этих коэффициентов в новых координатах
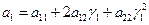 ;
; 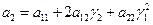 ;
;
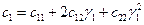 ;
; 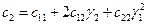 ;
;
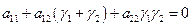 ;
; 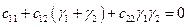 .
.
Последние два выражения позволяют вычислить формы собственных колебаний
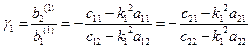
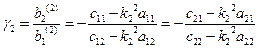
Таким образом, мы показали, что существуют такие координаты 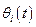 , в которых дифференциальные уравнения колебаний разделяются:
, в которых дифференциальные уравнения колебаний разделяются:
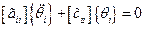 ,
, 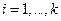 .
.
Каждое уравнение выглядит так, как уравнение колебаний механической системы с одной степенью свободы. Эти координаты называются главными. Если есть произвольный набор координат, для которых найдены формы и частоты свободных колебаний, то можно построить матрицу преобразования 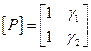 . Строки этой матрицы состоят из коэффициентов форм колебаний. Сами главные координаты находятся по правилу
. Строки этой матрицы состоят из коэффициентов форм колебаний. Сами главные координаты находятся по правилу
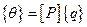 .
.
Матрица жесткости в главных координатах является диагональной:
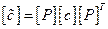 .
.
Матрица масс в главных координатах, также является диагональной:
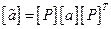 .
.
Если речь идет о вычислении амплитуд установившихся вынужденных колебаний, то матрица правых частей (возмущающих сил) строится по правилу
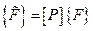 .
.
При этом система уравнений, описывающая вынужденные колебания, распадается на отдельные независимые уравнения:
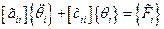 ,
, 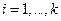 .
.
ПРИМЕР 6. Найти закон вынужденных колебаний механической системы, представленной на рис.3.14, используя главные координаты. Все необходимые величины указаны на рисунке.

Рис. 3.14
РЕШЕНИЕ. Используя в качестве обобщенных координат координаты материальных точек, введем в рассмотрение матрицу - столбец обобщенных координат
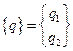
Для получения матриц инерции, жесткости и возмущающего силового воздействия используем решение примера 1:
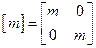 ;
; 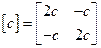 ;
; 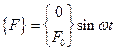 .
.
Для этой задачи ранее были вычислены формы собственных колебаний:
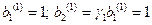 - первая форма, соответствующая частоте
- первая форма, соответствующая частоте 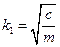 ;
;
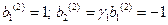 - вторая форма, соответствующая частоте
- вторая форма, соответствующая частоте 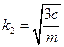 .
.
Используя формы собственных колебаний, записываем матрицу преобразований
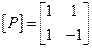 .
.
Переходим к главным координатам 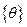
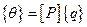 ;
; 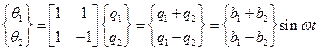 .
.
Строим матрицы для новых обобщенных коэффициентов инерции и жесткости
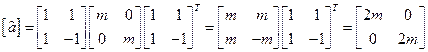 ;
;
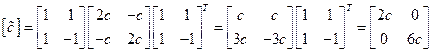 .
.
Строим новую матрицу – столбец возмущающих сил
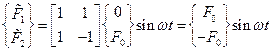 .
.
Записываем уравнения движения в главных координатах:
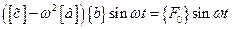 .
.
Решение этого уравнения разыскиваем в виде
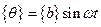
После подстановки решения в уравнение движения имеем
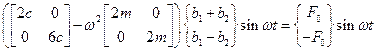 .
.
В результате приходим к двум независимым алгебраическим уравнениям:
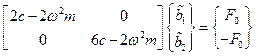 ,
,
Отсюда находим амплитуды установившихся вынужденных колебаний:
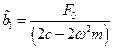 ;
; 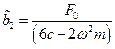 .
.
Решение для установившихся колебаний в главных координатах записывается в виде
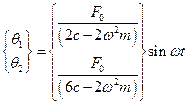 .
.
Дата добавления: 2016-02-11; просмотров: 3868;
