Вынужденные колебания консервативной системы с конечным числом степеней свободы при силовом гармоническом воздействии.

Запишем в матричной форме дифференциальные уравнения движения линейной консервативной системы:

,

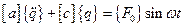где 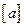- матрица обобщенных коэффициентов инерции; 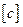- матрица обобщенных коэффициентов жесткости; 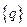- матрица –столбец обобщенных координат; 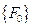- матрица - столбец амплитуд обобщенных сил.

Решение уравнения разыскивается в виде

,

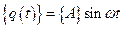где 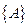- матрица – столбец амплитуд вынужденных колебаний.

Обобщенное ускорение будет равно

.

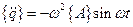В результате подстановки, находим

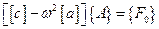. (3.13)

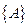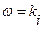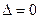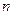Из системы неоднородных алгебраических уравнений находим матрицу - столбец амплитуд вынужденных колебаний . Следует учесть, что при главный определитель системы уравнений равен нулю: . Тогда по правилу Крамера, если вспомогательные определители не нули, мы получим бесконечный вектор-столбец . Типичный вид амплитудно-частотной характеристики для механической системы с степенями свободы представлен на рисунке (3.7).

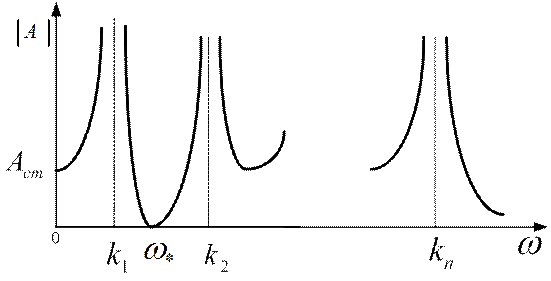
Рис.3.7

Если при некотором значении частоты 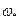, амплитуда 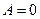, то говорят о явлении антирезонанса. В технике это понятие используется для виброзащиты конструкции.

Основные соотношения для системы с двумя степенями свободы:

Матрица обобщенных жесткостей и матрица обобщенных масс записывают соответственно в виде:

; .

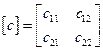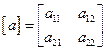Матрица-столбец обобщенных координат представляется как

.

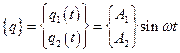Матрица-столбец силового возмущающего воздействия записывается в аналогичной форме

.

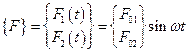Сравнивая коэффициенты у одинаковых тригонометрических функций в левой и правой частях матричного уравнения движения, получаем

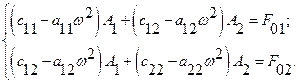(3.14)

Воспользуемся правилом Крамера, для этого вычислим соответствующие определители

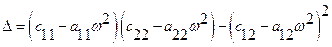
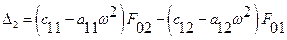
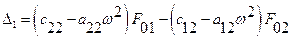
Амплитуды колебаний, соответствующие первой и второй обобщенным координатам, находятся из выражений

;

.

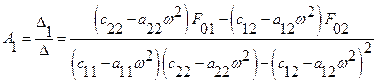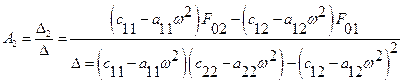Законы изменения обобщенных координат при установившихся вынужденных колебаниях представляются в форме

, .

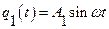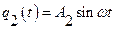ПРИМЕР 4. Заданны радиусы 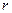и массы 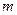двух одинаковых однородных цилиндров, центры которых соединены пружиной жесткостью 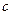(рис.3.8). К оси правого цилиндра приложена гармоническая возмущающая сила 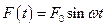. При качении цилиндров проскальзывание отсутствует. Построить амплитудно-частотную характеристику установившегося колебательного процесса.

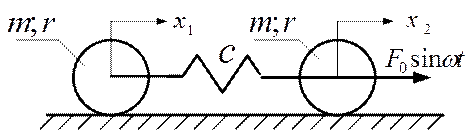
Рис. 3.8

РЕШЕНИЕ. В качестве обобщенных координат примем координаты: 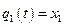, , 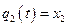определяющие положения центров цилиндров. Запишем выражение для кинетической энергии

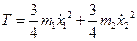
и найдем обобщенные коэффициенты инерции:

; ; .

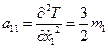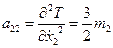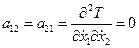Запишем выражение для потенциальной энергии пружины 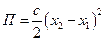и найдем обобщенные коэффициенты жесткости:

; ;

.

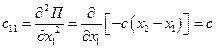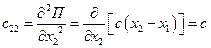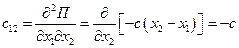Воспользуемся матричным представлением решения задачи в виде

.

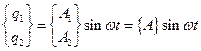Тогда уравнение колебательного движения можно записать так

,

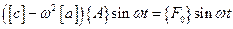где 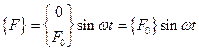- матричное представление внешнего силового воздействия. В результате приходим к матричной форме системы алгебраических уравнений:

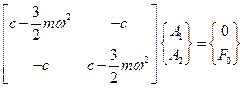. (3.15)

1. Амплитуды колебаний вычисляем по правилу Крамера

;

.

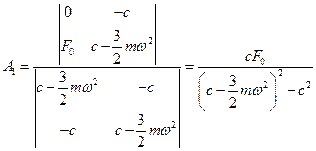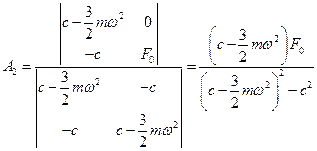2. Для составления частотного уравнения приравняем к нулю определитель квадратной матрицы из уравнения (3.15):

.

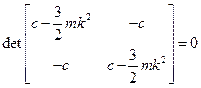Несложные преобразования

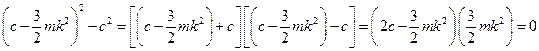
позволяют найти корни частотного уравнения

; .

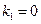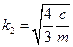3. Порядок построения амплитудно-частотной характеристики.

· Для определения экстремальных значений амплитуды 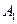найдем значения 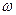, при которых производная знаменателя будет равна нулю:

.

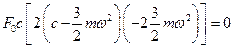Первому корню 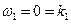этого уравнения, соответствует значение амплитуды равное 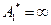, то есть достигается .

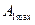Второму корню 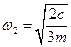соответствует значение амплитуды равное 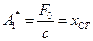, то есть достигается 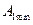. Заметим, что при подходе к значению 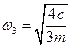справа амплитуда стремиться к 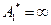, а при подходе слева – к 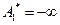. При стремлении 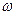к бесконечности отрицательная амплитуда стремиться к нулю.

· Для определения характера изменения амплитуды 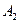проанализируем ее выражение:

.

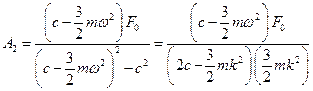Значению 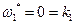соответствует значение амплитуды равно 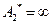, то есть достигается .

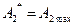Значению 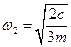, соответствует значение амплитуды равно .

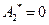При стремлении 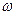к значению 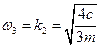слева амплитуда 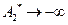, а при стремлении 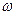к 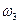справа 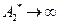. При стремлении 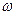к бесконечности положительная амплитуда стремиться к нулю.

На основании полученных данных строим амплитудно-частотную характеристику (рис.3.9).

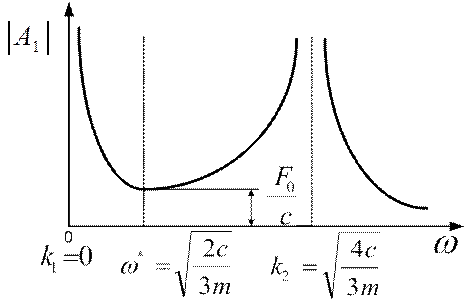
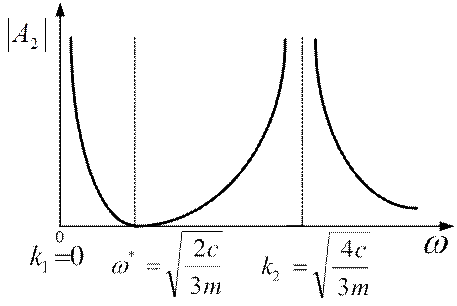
Рис. 3.9

ПРИМЕР 5. Плоский механизм (рис.3.10) состоит из тела, скользящего по наклонной плоскости, цилиндра, катящегося по другой наклонной плоскости и блока, вращающегося вокруг неподвижной оси. Все тела соединены между собой нерастяжимыми невесомыми нитями. Масса каждого твердого тела, входящего в плоский механизм, равна 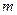, а радиусы цилиндрических тел одинаковые и равны 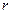. К телу, скользящему по наклонной плоскости приложена возмущающая сила 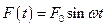. Построить амплитудно-частотную характеристику установившегося колебательного процесса.

Рис. 3.10

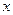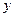РЕШЕНИЕ. В качестве обобщенных координат выберем величины и . Запишем выражение для кинетической энергии механизма:

.

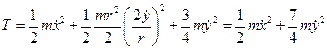Вычислим обобщенные коэффициенты инерции:

; ; .

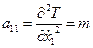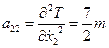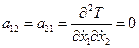Запишем матрицу инерции:

.

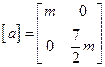При вычислении потенциальной энергии опустим слагаемое, соответствующее потенциальной энергии поля тяготения, так как оно не повлияет на величины коэффициентов обобщенной жесткости

.

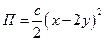Подсчитаем обобщенные коэффициенты жесткости:

; ;

.

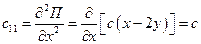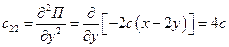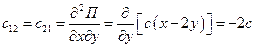Построим матрицу жесткости

.

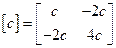Силового воздействия представим в матричной форме

.

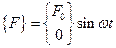Уравнение вынужденных колебаний механической системы запишем в виде

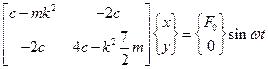. (3.16)

Ограничиваясь рассмотрением установившихся вынужденных колебаний, будем разыскивать решение уравнения в форме

.

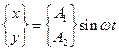Подставляем это решение в уравнение (3.16), в итоге приходим к системе неоднородных алгебраических уравнений:

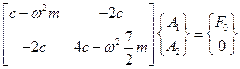. (3.17)

Используя правило Крамера, находим амплитуды вынужденных колебаний

;

.

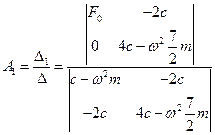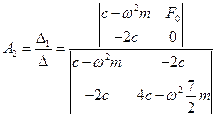Для определения собственных частот составим частотное уравнение, приравняв к нулю определитель матрицы уравнения (3.17)

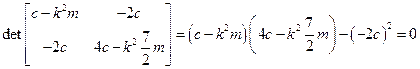
Его удобно переписать в виде

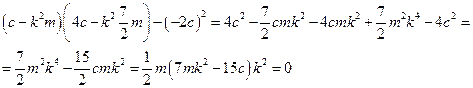
Откуда находим две собственные частоты

, .

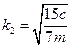Теперь выражения для амплитуд вынужденных колебаний можно переписать в более удобном для анализа виде:

;

.

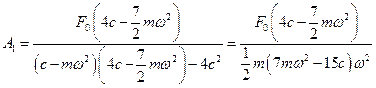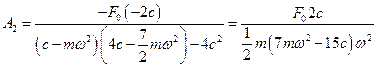Модули амплитуды колебани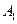й и 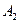достигают минимальных значени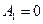й и 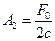при частоте возмущающего воздействия 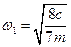. Те же амплитуды неограниченно возрастают при частотах возмущающего воздействия 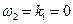и .

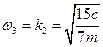Полученные данные позволяют построить амплитудно-частотную характеристику (рис.3.9) для рассматриваемой колебательной системы.

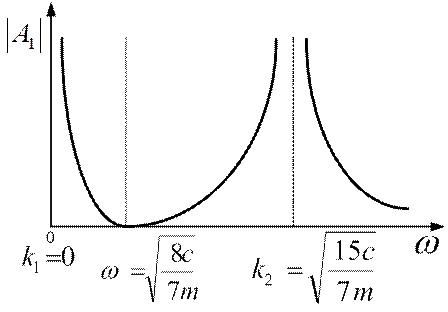
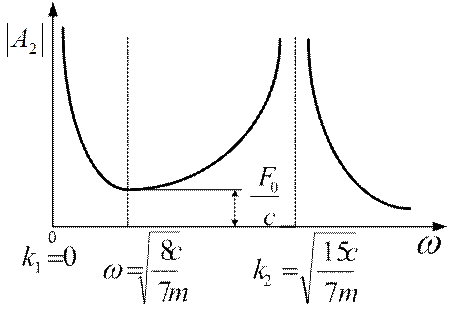
Рис. 3.11