Система с линейно-вязким сопротивлением при произвольной нагрузке.

По сравнению с предыдущим случаем уравнение движения системы дополняется слагаемым, учитывающим линейно-вязкое сопротивление, поэтому оно принимает вид

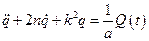(2.22)

Будем считать, что сопротивление мало, 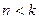. Воспользуемся подстановкой 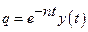, тогда обобщенная скорость и обобщенное ускорения будут равны:

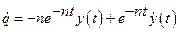и .

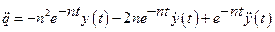Подставляя их значения в уравнение (2.22), найдем

.

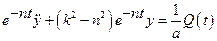Пусть 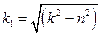- условная частота, тогда предыдущее уравнение принимает вид

.

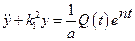Воспользуемся результатами предыдущего параграфа и запишем решение этого уравнения в форме

.

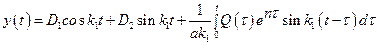С учетом использованной подстановки решение исходного уравнения (2.22) можно записать так:

.

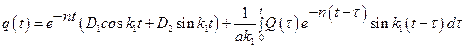Воспользуемся начальными условиями 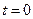: 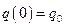; 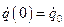для определения постоянных интегрирования

; .

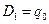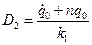Окончательное решение уравнения (2.22) представим как сумму двух видов колебаний:

1. Затухающие свободные колебания:

.

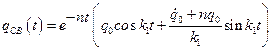Возникают в результате начальных возмущений и происходят с условной частото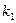й . При 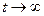амплитуда .

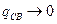2. Установившиеся вынужденные колебания, описываемые выражением

.

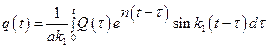Колебания систем с конечным числом степеней свободы.