Вынужденные колебания в случае непериодической возмущающей силы.
Уравнение движения при отсутствии сопротивления для механической системы с одной степенью свободы записывается в виде
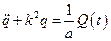 , (2.16)
, (2.16)
где 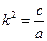 - квадрат круговой частоты свободных колебаний,
- квадрат круговой частоты свободных колебаний, 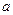 - обобщенный инерционный коэффициент,
- обобщенный инерционный коэффициент, 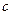 - обобщенный коэффициент жесткости,
- обобщенный коэффициент жесткости, 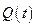 - обобщенная сила.
- обобщенная сила.
Решение предполагаем искать в виде :
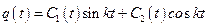 , (2.17)
, (2.17)
где 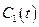 и
и 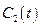 - неизвестные функции времени.
- неизвестные функции времени.
Обобщенная скорость находится дифференцированием (2.17):
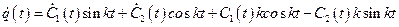 .
.
Воспользуемся методом вариации произвольных постоянных. «Постоянные» 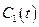 и
и 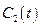 можно связать дополнительным условием: потребуем, чтобы выражение для
можно связать дополнительным условием: потребуем, чтобы выражение для 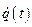 имело тот же вид, что и при постоянных
имело тот же вид, что и при постоянных 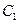 и
и 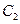 , не зависящих от времени, т.е.
, не зависящих от времени, т.е.
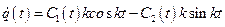 . (2.18)
. (2.18)
Тогда должно выполняться равенство:
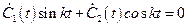 . (2.19)
. (2.19)
Дифференцируя выражение (2.18), найдем ускорение
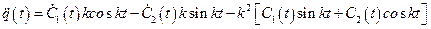 . (2.20)
. (2.20)
Подставляя (2.17) и (2.20) в (2.16), найдем, что
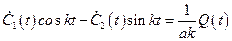 . (2.21)
. (2.21)
Уравнения (2.19) и (2.21) образуют систему неоднородных уравнений, содержащую две неизвестные функции 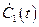 и
и 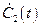 . Определитель этой системы отличен от нуля (
. Определитель этой системы отличен от нуля ( 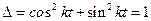 ), поэтому система не вырожденная. Ее решение находим с помощью правила Крамера:
), поэтому система не вырожденная. Ее решение находим с помощью правила Крамера:
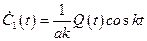 ;
; 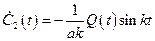 .
.
Интегрируем эти выражения:
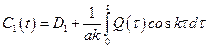 ;
; 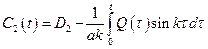 .
.
Здесь 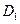 и
и 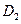 - произвольные постоянные, равные значениям
- произвольные постоянные, равные значениям 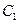 и
и 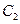 при
при 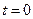 . Используя (2.17), (2.18) и начальные условия (
. Используя (2.17), (2.18) и начальные условия ( 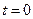 :
: 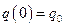 ,
, 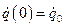 ), находим:
), находим: 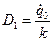 и
и 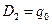 . Общее решение запишется в виде
. Общее решение запишется в виде
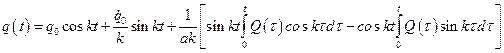
или в более компактной форме:
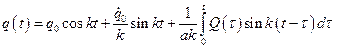 .
.
При нулевых начальных условиях 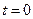 :
: 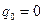 ;
; 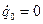 (в начальный момент система покоилась) решение упрощается:
(в начальный момент система покоилась) решение упрощается:
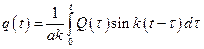 .
.
Дата добавления: 2016-02-11; просмотров: 859;
