Колебания системы с одной степенью свободы при линейно- вязком сопротивлении.

Уравнение движения колебательной системы, на которую действуют силы сопротивления, пропорциональные скорости, записывается в виде

.

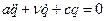Чаще используют другую форму записи:

,

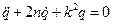где 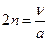- коэффициент сопротивления, а 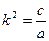- частота свободных колебаний. Решение этого уравнения при малом сопротивлении ( 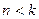) разыскивается в виде

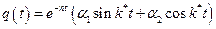. (2.6)

Здесь и - постоянные интегрирования; - круговая частота затухающих колебаний. Если это неравенство не выполняется, процесс движения будет апериодическим, и решение ищут как комбинацию экспоненциальных функций.

Используя решение (2.6), запишем выражение для обобщенной скорости:

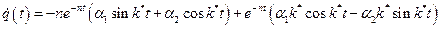. (2.7)

Для нахождения постоянных интегрирования и нужно воспользоваться начальными условиями 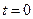: , , 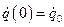подставив их в выражения (2.6) и (2.7). В результате приходим к системе алгебраических уравнений:

; (2.8)

. (2.9)

Разрешая уравнения (2.8) и (2.9) относительно и , находим

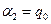и .

Тогда решение (2.6) можно записать виде

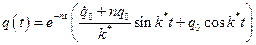
или

,

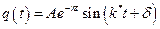где - амплитуда колебаний; - начальная фаза, которая определяется из соотношения 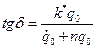. Типичный процесс движения показан на графике (рис.2.12).

Рис.2.12

Процесс движения непериодический, однако, нули функции 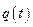повторяются периодически, поэтому можно говорить об условном периоде 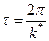. Асимптота процесса определяется формулой , при этом амплитуды колебаний образуют геометрическую прогрессию с постоянным коэффициентом затухания 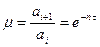. Сколько бы не продолжался процесс, формально он никогда не исчезнет. Но практически процессы с трением исчезают всегда.

ПРИМЕР 6. Механическая система, состоящая из двух соосных (насаженных неподвижно на единую ось) блоков, груза и однородного диска, прикрепленных соответственно к неподвижному основанию пружиной и демпфером (см. рис.2.13), находится в положении статического равновесия. Зная жесткость пружины , осевой момент инерции соосного блока 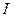, веса груза и диска, а так же радиусы блоков и диска, найти закон движения груза. В начальный момент механизм покоился, а пружина была сжата на величину 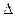, то есть при : , .

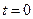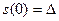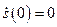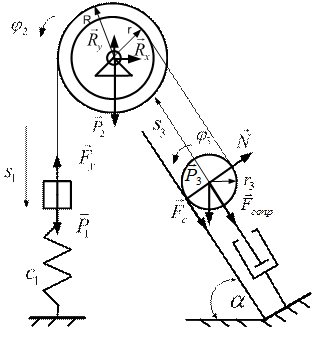
Рис.2.13

РЕШЕНИЕ. Для составления дифференциального уравнения воспользуемся уравнениями Лагранжа второго рода в форме

,

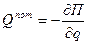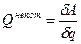где - обобщенная координата, а и - обобщенные силы для потенциальных и не потенциальных сил соответственно . Запишем уравнения кинематических связей:

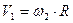или ;

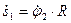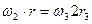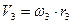или ;

или .

При записи учтено, что мгновенный центр скоростей диска, катящегося без скольжения, расположен в точке его соприкосновения с плоскостью. Составим выражение для кинетической энергии механической системы:

.

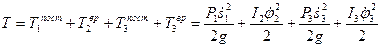Воспользовавшись уравнениями кинематических связей, вынесем за скобки квадрат величины , представив кинетическую энергию как квадратичную функцию обобщенной скорости:

.

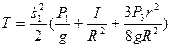При получении результата учтено, что осевой момент инерции однородного диска равен 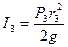. Частная производная от кинетической энергии по обобщенной координате будет равна нулю, так как она не зависит от обобщенной координаты. Частная производная от кинетической энергии по обобщенной скорости будет равна:

.

Производная по времени от частной производной кинетической энергии по обобщенной скорости:

.

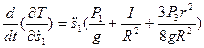Запишем выражение для потенциальной энергии механической системы как работу потенциальных сил по переводу системы из отклоненного положения в начальное

.

Для вычисления обобщенной силы 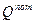продифференцируем это выражение по обобщенной координате:

.

При получении выражения учтено, что в положении статического равновесия и .

Для вычисления обобщенной силы сообщим системе возможное перемещение. Составим сумму работ не потенциальных внешних сил (сила 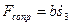) на соответствующем возможном перемещении и вынесем вариацию обобщенной координаты за скобки:

.

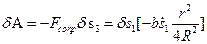Выражение в квадратных скобках и есть обобщенная сила для выбранной обобщенной координаты. После подстановки в уравнение Лагранжа второго рода выражений для частных производных кинетической энергии и обобщенных сил, получим искомое дифференциальное уравнение в виде ,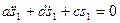

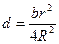где и - постоянные коэффициенты. Решение этого уравнения легко получить, если его записать в канонической форме:

,

где частота собственных колебаний; 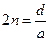- коэффициент сопротивления. Согласно полученным выше теоретическим результатам при 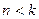решение последнего дифференциального уравнения будет:

,

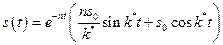где 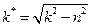- частота затухающих колебаний.

2.5. Вынужденные колебания системы при силовом гармоническом вынуждающем воздействии.

Рассмотрим упругую механическую систему с одной степенью свободы, к которой приложено силовое гармоническое воздействие. Воздействие называется гармоническим, если приложенная сила изменяется по закону или 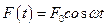. В первом случае дифференциальное уравнение движения системы приводится к виду

,

где 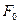- амплитуда обобщенной силы. Общий интеграл записывается в форме

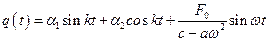. (2.10)

Используя начальные условия 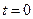: 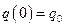, 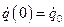и выражение для скорости

,

найдем постоянные интегрирования:

; .

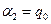Подставим значения этих постоянных в решение (2.10)

. (2.11)

Проанализируем выражение (2.11). Это решение содержит слагаемые, соответствующие свободным колебаниям

,

и вынужденным колебаниям

.

Кроме того, в решении присутствуют колебания, амплитуда которых обусловлена вынуждающим воздействием, а частота совпадает с частотой свободных колебаний :

.

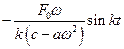Последнюю часть обычно называют сопровождающими колебаниями. Вынужденные колебания происходят с частотой вынуждающей силы и амплитудой 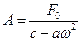. В чистом виде они реализуются только при специальном выборе начальных условий, когда 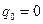и 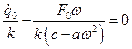. Обычно, вследствие наличия сил трения (сопротивления), свободные и сопутствующие колебания по истечении некоторого промежутка времени затухают, и механическая система совершает только вынужденные колебания.

Запишем зависимость амплитуды вынужденных колебаний от частоты вынуждающего воздействия

,

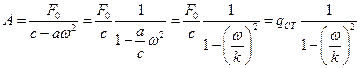где 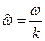- безразмерная частота вынуждающего воздействия, а 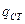- статическое значение обобщенной координаты 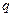. Обычно амплитудно-частотной характеристикой механической системы называют модуль полученного выражения.

Типичный вид амплитудно-частотной характеристики представлен на рисунке (2.14).

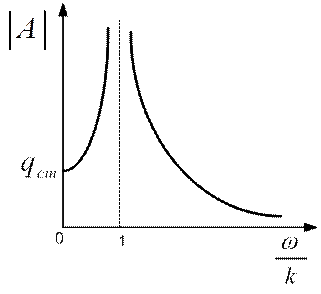
Рис.2.14

Точка разрыва с физической точки зрения не реальна. Можно показать, что в этом случае решение носит качественно другой характер и имеет вид 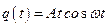. Это колебания с линейно нарастающей амплитудой.

Существует понятие коэффициента динамичности, который равен модулю отношения максимального динамического отклонения к статическому

.

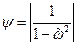Его зависимость от относительной частоты представлена на рис.2.15.

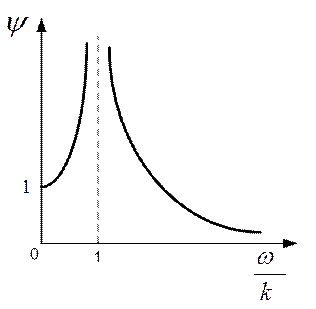
Рис. 2.15

Коэффициент динамичности часто используется в технических расчетах для оценки напряженно-деформированного состояния механизмов и конструкций, испытывающих динамические нагрузки.

2.6. Вынужденные колебания вязкоупругой системы при силовом гармоническом воздействии.

Дифференциальное уравнение движения для таких систем, если они линейны, имеет вид

или

.

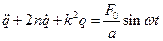Общий интеграл записывается в форме

,

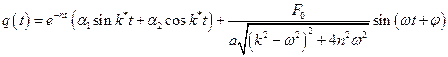где 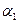и - постоянные интегрирования, которые определяются из начальных условий; 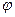- сдвиг фаз между вынужденными колебаниями и вынуждающей силой. Его величину можно установить из соотношения:

.

При любых 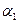и , т.е. при любых начальных условиях, с течением времени ( ) остается только часть решения

,

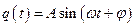которую называют установившимися вынужденными колебаниями. Амплитуда вынужденных колебаний определяется выражением

,

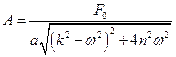или в более удобной форме

.

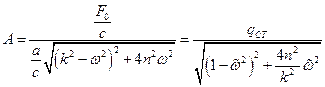Амплитудно-частотная характеристика вынужденных колебаний представлена на рис.2.16.

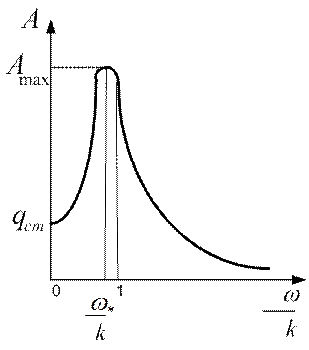
Рис.2.16

В упругой системе резонанс наступал в случае, когда частота собственных колебаний совпадала с частотой вынуждающего воздействия . В системе с вязким трением это не так; при значение амплитуды равно , но оно не достигает максимума. Для определения максимальной амплитуды необходимо решить уравнение 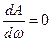, из него определяется частота 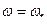силового воздействия, при котором . В данном случае это уравнение выглядит так

.

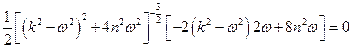Приравняв числитель выражения к нулю, и выполнив ряд несложных алгебраических преобразований, получаем, что ; откуда .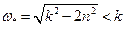

Максимальная амплитуда равна .

Коэффициент динамичности изменяется в зависимости от частоты по закону 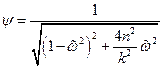. График изменения модуля коэффициента динамичности от относительной частоты представлен на рис.2.17.

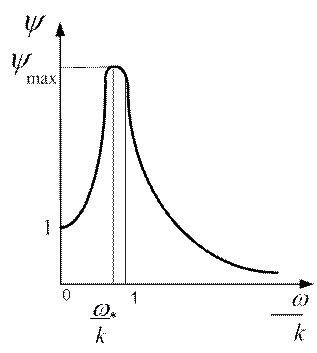
Рис.2.17