Вынужденные колебания в случае периодической возмущающей силы.

Дифференциальное уравнение движения механической системы с одной степенью свободы, совершающей вынужденные колебания, записывается в виде

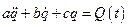, (2.12)

где 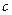- обобщенная жесткость; 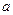- обобщенный коэффициент инерции;
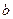- обобщенный коэффициент демпфирования; 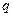- обобщенная координата; 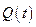- обобщенная сила.

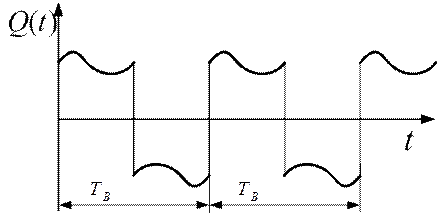
Рис. 2.18

Будем считать, что функция 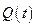(рис.2.18) удовлетворяет условиям Дирихле, то есть ее величина ограничена, а на конечном интервале, где она определена, имеются лишь разрывы первого рода и конечное число экстремумов. При этих условиях функцию 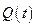можно разложить в ряд Фурье:

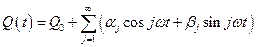, (2.13)

где ; ; ; .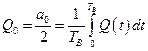

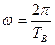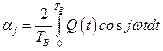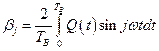Выражение (2.13) можно представить в более удобной форме

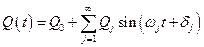, (2.14)

где ; ; .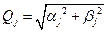

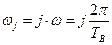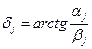Каждый член ряда (2.14) называется гармоникой. Подставляя (2.14) в (2.12), приходим к уравнению

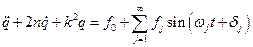, (2.15)

где 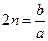- коэффициент сопротивления; 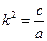- квадрат круговой частоты свободных колебаний.

Решение дифференциального уравнения (2.15) состоит из общего решения однородного уравнения и частного решения неоднородного уравнения. Общее решение зависит от начальных условий и в силу наличия вязкого сопротивления затухает с течением времени. Поэтому ограничимся рассмотрением установившихся вынужденных колебаний, которые полностью описываются частным решением

.

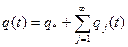Здесь 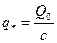- постоянная величина, а функции 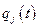целесообразно записать в виде

,

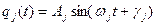где 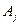- амплитуда; 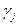- сдвиг фаз 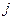-ой гармоники установившихся гармонических колебаний:

; .

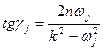В силу кратности частот 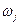установившиеся вынужденные колебания будут периодическими и происходят с периодом .

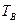Последовательность амплитуд 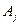характеризуется дискретным линейчатым спектром (2.19).

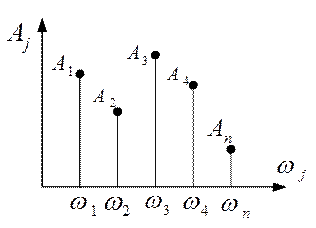
Рис.2.19

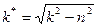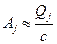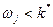Сама колебательная система ведет себя как фильтр. Она пропускает почти без искажения гармоники с частотами много меньшими резонансной частоты ( , для ) и усиливает гармоники с частотами, близкими к резонансным ( 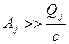для 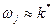), и, наконец, она не пропускает гармоники с частотами много большими, чем частота резонанса, то есть 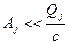для 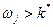(рис.2.20).

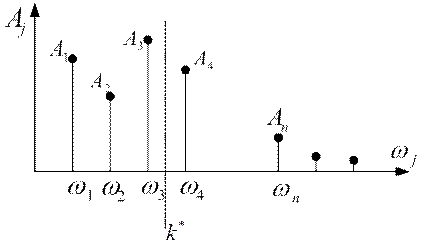
Рис. 2.20