Критерий устойчивости положения равновесия.
Для ответа на вопрос, имеет ли механическая система положения равновесия, часто используют принцип возможных перемещений. Он утверждает, что если на механическую систему с 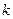 степенями свободы наложены идеальные голономные связи, то необходимым и достаточным условием равновесия является равенство нулю всех обобщенных сил
степенями свободы наложены идеальные голономные связи, то необходимым и достаточным условием равновесия является равенство нулю всех обобщенных сил
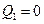 ,
, 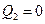 , …,
, …, 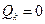 .
.
Если на систему действуют только консервативные силы, то 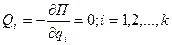 ,
,
где 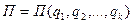 - потенциальная энергия.
- потенциальная энергия.
Теорема Лагранжа-Дирихле утверждает: в положении устойчивого равновесия потенциальная энергия должна иметь локальный минимум. При этом предполагается, что на систему наложены голономные идеальные стационарные связи, а заданные силы не зависят от времени (являются потенциальными).
Будем считать, что положение равновесия определяется нулевыми значениями обобщенный координат 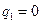 ,
, 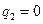 , …,
, …, 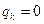 . Рассмотрим бесконечно малые отклонения системы от положения равновесия
. Рассмотрим бесконечно малые отклонения системы от положения равновесия 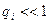 . Разложим потенциальную энергию в близи положения равновесия в ряд Маклорена
. Разложим потенциальную энергию в близи положения равновесия в ряд Маклорена
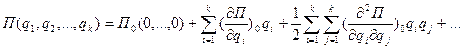
Начало отсчета потенциальной энергии выбираем в положении равновесия , тогда 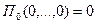 . В положении равновесия потенциальная энергия достигает минимального значении, поэтому
. В положении равновесия потенциальная энергия достигает минимального значении, поэтому 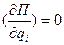 . Следовательно, потенциальная энергия в окрестности положения равновесия может быть представлена в виде
. Следовательно, потенциальная энергия в окрестности положения равновесия может быть представлена в виде
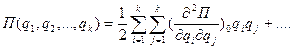 ,
,
где 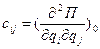 - обобщенные коэффициенты жесткости.
- обобщенные коэффициенты жесткости.
Отбрасывая члены высшего порядка малости, потенциальную энергию можно записать в виде
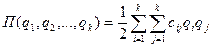 .
.
Вывод: для существования минимума потенциальной энергии в окрестности положения равновесия она должна быть определенно положительной квадратичной формой (рис.2.4).
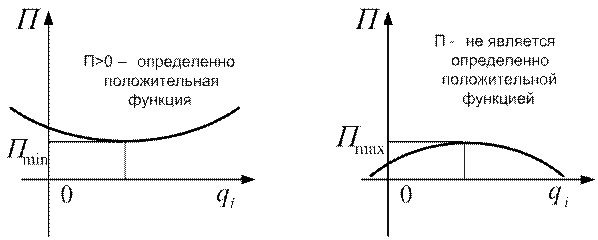
Рис.2.4
В соответствии с критерием Сильвестра необходимым и достаточным условием определенной положительности квадратичной формы (в рассматриваемом случае - потенциальной энергии) является требование, чтобы все главные миноры определителя матрицы обобщенных коэффициентов жесткости 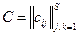 были положительны
были положительны
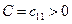 ;
; 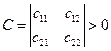 ; …,
; …, 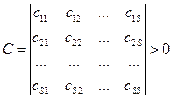 . (2.1)
. (2.1)
Процедура проверки устойчивости положения равновесия на основе теоремы Лагранжа-Дирихле состоит в следующем:
- потенциальная энергия раскладывается в ряд с точностью до членов второго порядка малости в окрестности положения равновесия;
- составляется матрица коэффициентов жесткости;
- вычисляются главные миноры (2.1) и анализируются их знаки.
ПРИМЕР 1. Определить положения равновесия физического маятника (рис.2.5).
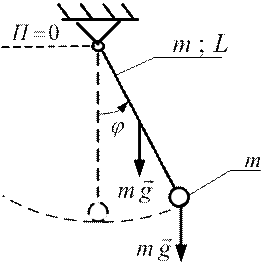
Рис.2.5
РЕШЕНИЕ. Вычислим потенциальную энергию
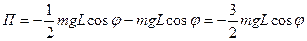
Условие равновесия в обобщенных силах:
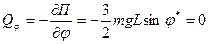
Корни этого уравнения 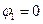 и
и 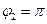 определяют положения равновесия маятника. Обобщенный коэффициент жесткости вычисляется по формуле
определяют положения равновесия маятника. Обобщенный коэффициент жесткости вычисляется по формуле
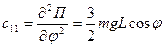 .
.
Значение 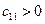 положительно при
положительно при 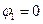 , значит при этом значении угла положение равновесия маятника устойчивое, а при
, значит при этом значении угла положение равновесия маятника устойчивое, а при 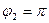 коэффициент
коэффициент 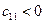 , что соответствует неустойчивому положению равновесия.
, что соответствует неустойчивому положению равновесия.
ПРИМЕР 2. Определить положения равновесия однородного стержня массой 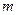 и длиной
и длиной 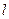 , прикрепленного к плоскости шарниром и спиральной пружиной жесткости
, прикрепленного к плоскости шарниром и спиральной пружиной жесткости 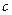 (рис.2.6) и выполнить анализ их устойчивости. В верхнем вертикальном положении стержня пружина не деформирована.
(рис.2.6) и выполнить анализ их устойчивости. В верхнем вертикальном положении стержня пружина не деформирована.
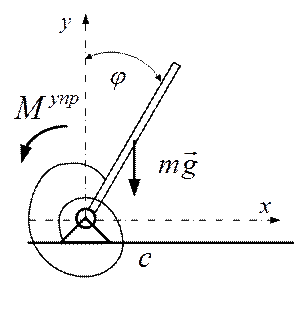
Рис.2.6
РЕШЕНИЕ. Система имеет одну степень свободы. В качестве обобщенной координаты выберем угол 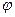 отклонения от вертикали. Запишем выражение для потенциальной энергии, как работу по переводу системы из отклоненного положения в исходное (вертикальное):
отклонения от вертикали. Запишем выражение для потенциальной энергии, как работу по переводу системы из отклоненного положения в исходное (вертикальное):
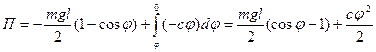 .
.
Здесь учтено, что пружина создает момент 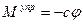 , препятствующий углу отклонения. Составим уравнение равновесия:
, препятствующий углу отклонения. Составим уравнение равновесия:
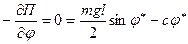 ,
,
Здесь 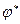 - значение угла отклонения в положении равновесия. Заметим, что это уравнение представляет собой сумму моментов действующих на стержень усилий относительно опорного шарнира. Решение полученного трансцендентного уравнения удобно выполнить графически (рис.2.7), находя решение в виде точек пересечения двух функций – момента опрокидывающего, равного
- значение угла отклонения в положении равновесия. Заметим, что это уравнение представляет собой сумму моментов действующих на стержень усилий относительно опорного шарнира. Решение полученного трансцендентного уравнения удобно выполнить графически (рис.2.7), находя решение в виде точек пересечения двух функций – момента опрокидывающего, равного 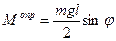 , и момента восстанавливающего, равного
, и момента восстанавливающего, равного 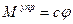 .
.
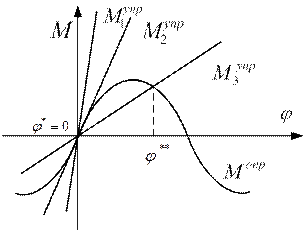
Рис.2.7
Анализ рисунка показывает, что при 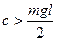 прямая
прямая 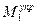 восстанавливающего момента пересекает синусоиду опрокидывающего момента только в одной точке
восстанавливающего момента пересекает синусоиду опрокидывающего момента только в одной точке 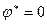 , т.е. вертикальное положение стержня является его положением равновесия. При
, т.е. вертикальное положение стержня является его положением равновесия. При 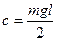 касательная к
касательная к 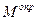 совпадает с прямой
совпадает с прямой 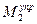 ; это говорит о существовании в окрестности
; это говорит о существовании в окрестности 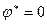 небольшого интервала значений углов отклонения, при которых будет иметь место равновесие стержня. В случае, когда
небольшого интервала значений углов отклонения, при которых будет иметь место равновесие стержня. В случае, когда 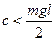 , прямая
, прямая 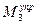 пересекает синусоиду
пересекает синусоиду 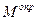 в нескольких точках, что говорит о наличии у рассматриваемой механической системы нескольких положений равновесия.
в нескольких точках, что говорит о наличии у рассматриваемой механической системы нескольких положений равновесия.
Найдем условие, при котором вертикальное положение стержня будет устойчиво. Сначала разложим функцию потенциальной энергии в ряд по степеням 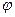 :
:
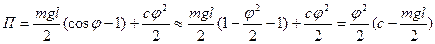
По условию (2.1) вертикальное положение стержня будет устойчиво, если будет положителен обобщенный коэффициент жесткости; последнее утверждение будет справедливо при условии 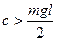 , что соответствует случаю
, что соответствует случаю 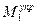 на рис.2.7.
на рис.2.7.
Теперь проанализируем вертикальное положение равновесия, сопоставив величины опрокидывающего и восстанавливающего моментов.
В случае, когда 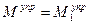 , дадим стержню небольшое отклонение
, дадим стержню небольшое отклонение 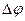 вправо от вертикального положения равновесия, после чего внешнее воздействие прекратим. Из рисунка 2.7 видно, что в этом случае
вправо от вертикального положения равновесия, после чего внешнее воздействие прекратим. Из рисунка 2.7 видно, что в этом случае 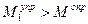 , и стержень будет возвращаться в исходное положение. Если дать стержню небольшое отклонение
, и стержень будет возвращаться в исходное положение. Если дать стержню небольшое отклонение 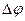 влево, то
влево, то 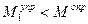 , и стержень будет снова возвращен в исходное положение. Вывод: в случае, когда
, и стержень будет снова возвращен в исходное положение. Вывод: в случае, когда 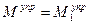 вертикальное положение стержня – устойчивое.
вертикальное положение стержня – устойчивое.
Рассуждая аналогично, нетрудно понять, что в случае, когда 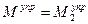 , положение стержня оказывается безразличным, так как при небольшом отклонении
, положение стержня оказывается безразличным, так как при небольшом отклонении 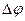 влево или вправо имеет место равенство
влево или вправо имеет место равенство 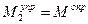 (при увеличении значения
(при увеличении значения 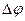 равенство нарушается).
равенство нарушается).
В случае, когда 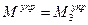 вертикальное положение стержня
вертикальное положение стержня 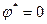 оказывается неустойчивым, поскольку небольшое отклонение
оказывается неустойчивым, поскольку небольшое отклонение 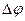 приводит к возрастанию отклонения, так как
приводит к возрастанию отклонения, так как 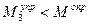 (см. рис.2.7). Возрастание отклонения будет продолжаться, пока отклонение стержня не достигнет величины
(см. рис.2.7). Возрастание отклонения будет продолжаться, пока отклонение стержня не достигнет величины 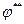 (следующее положение равновесия). Анализ графиков моментов показывает, что при дальнейшем отклонении от нового положения равновесия вправо на небольшую величину
(следующее положение равновесия). Анализ графиков моментов показывает, что при дальнейшем отклонении от нового положения равновесия вправо на небольшую величину 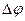 имеет место неравенство
имеет место неравенство 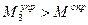 , что свидетельствует о стремлении стержня вернуться в пройденное положение равновесия. При отклонении от нового положения равновесия влево на небольшую величину
, что свидетельствует о стремлении стержня вернуться в пройденное положение равновесия. При отклонении от нового положения равновесия влево на небольшую величину 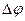 имеет место неравенство
имеет место неравенство 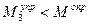 , что свидетельствует о стремлении стержня увеличить угол отклонения до величины
, что свидетельствует о стремлении стержня увеличить угол отклонения до величины 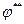 . На основании анализа можно сделать вывод, что в случае, когда
. На основании анализа можно сделать вывод, что в случае, когда 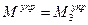 положение равновесия
положение равновесия 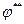 будет устойчивым, а вертикальное положение
будет устойчивым, а вертикальное положение 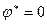 - неустойчивым.
- неустойчивым.
ПРИМЕР 3. При каком соотношении параметров показанное на рисунке 2.8 пунктиром положение равновесия упругой системы будет устойчивым?
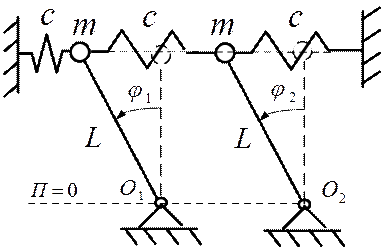
Рис.2.8
РЕШЕНИЕ. Запишем выражение для потенциальной энергии механической системы:
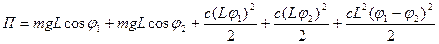 .
.
Вычислим обобщенные коэффициенты жесткости:
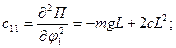
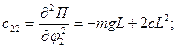
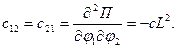
Матрицу обобщенных коэффициентов жесткости можно записать в виде
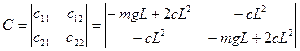 .
.
Условие положительности первого главного минора:
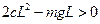 .
.
Условие положительности второго главного минора:
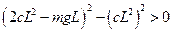 .
.
Из первого неравенства следует, что 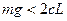 , а из второго – а)
, а из второго – а) 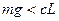 , б)
, б) 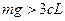 . Сравнивая соотношения приходим к выводу: равновесие системы устойчиво при
. Сравнивая соотношения приходим к выводу: равновесие системы устойчиво при 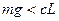 .
.
ПРИМЕР 4. Исследовать устойчивость вертикального положения равновесия системы маятников (см. рис. 2.9). Массы всех маятников и жесткости всех пружин одинаковы, массами стержней пренебречь. В показанном положении пружины не напряжены.
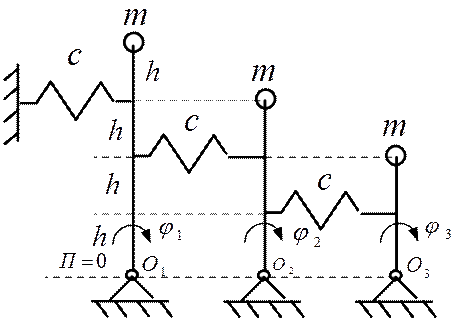
Рис.2.9
РЕШЕНИЕ. Запишем потенциальную энергию:
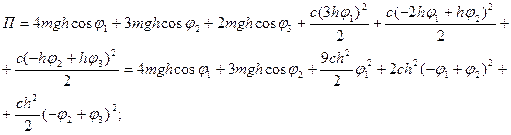
Вычислим обобщенные коэффициенты жесткости:
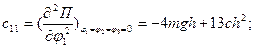
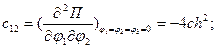
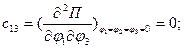
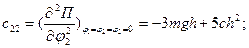
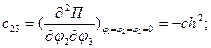
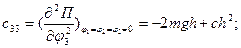
Составим матрицу обобщенных коэффициентов жесткостей:
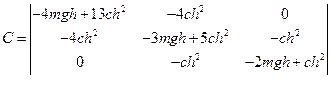 .
.
Условия устойчивости запишем как условия положительности главных миноров
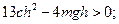
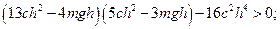
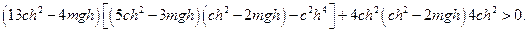
Первое условие выполняется при 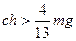 . Сравнительно несложные преобразования показывают, что при выполнении первого условия второе условие выполняется при
. Сравнительно несложные преобразования показывают, что при выполнении первого условия второе условие выполняется при 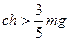 . При выполнении первых двух условий третье условие выполняется при
. При выполнении первых двух условий третье условие выполняется при 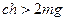 . Очевидно, что выполнение последнего условия приводит к автоматическому выполнению первых двух условий. Вывод: вертикальное положение стержней изображенной конструкции устойчиво при выполнении условия
. Очевидно, что выполнение последнего условия приводит к автоматическому выполнению первых двух условий. Вывод: вертикальное положение стержней изображенной конструкции устойчиво при выполнении условия 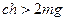 .
.
Дата добавления: 2016-02-11; просмотров: 4593;
