Свободные колебания механической системы с одной степенью свободы.

Рассмотрим консервативную систему с голономными и стационарными связями, имеющую одну степень свободы. Основные характеристики для таких механических систем вычисляются по формулам:

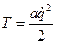- кинетическая энергия;

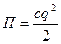- потенциальная энергия;

где 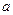- обобщенный коэффициент инерции; 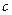- обобщенный коэффициент жесткости. В этом случае уравнение Лагранжа II-рода 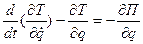приводится к виду

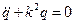, (2.2)

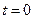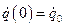где - круговая частота колебаний. Начальные условия , , позволяют записать решение дифференциального уравнения (2.2) в виде

.

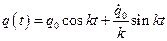Имеется эквивалентная форма записи

,

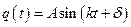где 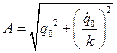- амплитуда колебаний; 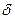- начальная фаза, которая определяется из соотношения 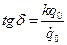. Процесс движения системы – гармонические колебания с периодом (рис.2.10).

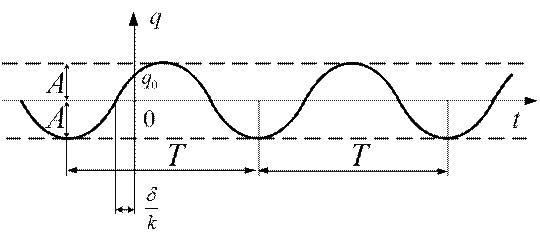
Рис.2.10

ПРИМЕР 5. Стержень веса 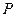положен на валки (см. рис.2.11), которые вращаются в разные стороны с одинаковой угловой скоростью 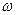. Расстояние между валками 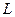, 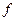- коэффициент трения скольжения стержня о валки. В начальный момент центр тяжести стержня находился на расстоянии 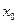от середины расстояния между валками, его скорость равнялась нулю. Затем его отпустили без начальной скорости. Определить закон движения стержня .

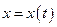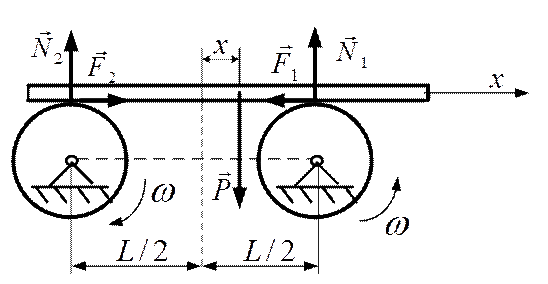
Рис.2.11

РЕШЕНИЕ. Составим уравнение движения балки:

; (2.3)

Уравнение равновесия сил в проекции на вертикальную ось

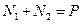; (2.4)

Уравнение равновесия моментов относительно левой опоры

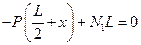. (2.5)

Последовательно исключаем из системы уравнений (2.3) - (2.5) неизвестные реакции:

; ;

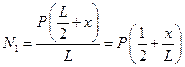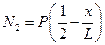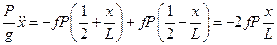
В результате дифференциальное уравнение движения балки примет вид

,

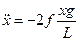Совпадающий с (2.2), где 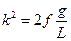- квадрат круговой частоты колебаний.

Используя начальные условия 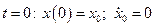, находим закон движения балки

.