В этом случае y* - оптимальное решение двойственной задачи.

Доказательство:

Достаточность. Пусть x*, y* - допустимые решения прямой и двойственной задач и <с, x*> = <b, y*>. Тогда для любого допустимого решения х по основной лемме имеем:

<с, x> ≤ <b, y*> = <с, x*>,

то есть <с, x> ≤ <с, x*> при любом допустимом x. Это и означает оптимальность решения x*.

С другой стороны, для любого допустимого решения y из основной леммы имеем:

<b,y> ≥ <c, x*>=<b, y*>, т. е. <b,y> ≥ <b, y*>,что и означает оптимальность y*.

Необходимость(без доказательства). Если х* - оптимальное решение задачи (Р), то в двойственной задаче обязательно найдется допустимый вектор y* такой, что значения целевых функций будут равны: <c, x*> = <b, y*>.

Эквивалентная формулировка первой теоремы (симметричная): Если одна из пары двойственных задач имеет оптимальное решение, то и другая задача также имеет оптимальное решение, причем оптимальные значения целевых функций (на оптимальных решениях) совпадают.

Лемма: Если целевая функция ∑bi yi в двойственной задаче (D) не ограничена снизу на множестве допустимых решений y, то прямая задача (Р) не имеет ни одного допустимого решения, то есть несовместна.

Доказательство:

Если бы задача (Р) имела допустимое решение х˚, то по основной лемме для любого допустимого решения y F(y) = ∑b_i y_i ≥ ∑ с_j x_j˚ = const, то есть F(y) ограничена снизу, что противоречит условию леммы. Противоречие доказывает лемму.

Замечание: Эту лемму можно использовать для установления факта несовместности задачи ЛП (то есть как достаточное условие несовместности).

Логически возможны три случая:

1) Обе задачи (Р) и (D) совместны;

2) Обе задачи несовместны;

3) Одна из задач совместна, а другая несовместна.

В последнем случае совместная задача не имеет решения, что может быть вызвано только неограниченностью целевoй функции. Действительно, если бы совместная задача была ограничена по целевой фунции, то она имела бы оптимальное решение. Но тогда по первой теореме двойственности имела бы решение и другая задача, что противоречит предположению пункта 3).

Следующие три примера показывают, что все три возможности осуществляются.

Примеры:

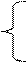
1) 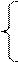2х₁ + х₂ ≤ 4 2y₁ + y₂ ≥ 1

x₁ + 2x₂ ≤ 4 y₁ + 2y₂ ≥ 1

x₁, х₂ ≥ 0 y₁, y₂ ≥ 0

Z(x)= x₁ + х₂ → max F(y)= 4y₁ + 4y₂ → min

Решите задачи геометрическим способом и убедитесь, что оптимальные решения

x* =( ⁴/₃, ⁴/₃ ), y* = ( ⅓, ⅓ ) и Z(x*) = F(y*)= ⁸/₃ .

Вывод: В этом примере обе задачи совместны и имеют оптимальное решение.

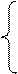2)х₁ - х₂ ≤ 3 y₁ - y₂ ≥ 1

-x₁ + x₂ ≤ -4 -y₁ + y₂ ≥3

x₁, х₂ ≥ 0 y₁, y₂ ≥ 0

Z(x)= x₁ + 3х₂ → max F(y)= 3y₁ -4y₂ → min

Легко видеть, что здесь обе задачи несовместны. Складывая неравенства, в первой из них получим 0 ≥-1, во второй 0 ≥4, что указывает на несовместность ограничений.

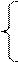
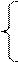3) х₁ - х₂ ≤ 1 y₁ ≥ 1

-y₁ ≥ 0

x₁, х₂ ≥ 0 y₁ ≥ 0

Z(x)= x₁ → max F(y)= y₁ → min

Здесь первая задача совместна, а вторая – несовместна. Сложив два неравенства, получим 0 ≥1. В соответствии с леммой первая задача должна не иметь оптимального решения. Действительно, она оказывается неограниченной сверху.