Теория двойственности в Линейном Программировании (ЛП).

Лекция 4.

Рассмотрим стандартную задачу ЛП (P) (с ограничениями-неравенствами) и связанную с ней так называемую двойственную к ней задачу (D):

Задача Р Задача D

A x ≤ b A^T y ≥ c

(m×n)(n×1)(m×1) (n×m)(m×1)( n×1)

x ≥ 0 y ≥ 0

<c, x> → max <b, y> → min

В покоординатном виде эти задачи имеют следующий вид (здесь и далее суммирование по индексу i от 1 до m , по j - от 1 до n):

Задача Р Задача D

∑ a_ij x_j ≤ b_i (i=1,…, m) ∑ a_ij y_i ≥ с_j = (j=1,…, n)

x_j ≥ 0 (j=1,…, n) y_i ≥ 0 (i=1,…,m)

∑c_jx _j → max ∑ b_i y_i → min (суммирование по j от 1 до n) (суммирование по i от 1 до m)

Ниже приведен «рецепт» построения двойственной задачи:

1). 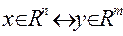; 2). c ↔ b; 3). max ↔ min; 4). A ↔ A^T 5). ≤ ↔ ≥

Утверждение. Задача, двойственная к двойственной, совпадает с исходной (с точностью до обозначений). (Доказать самостоятельно).

Задачи (P) и (D) тесно взаимосвязаны. Они называются взаимодвойственными. Совместный анализ этих задач позволяет легче найти решение и, главное, изучить качественные свойства решений. В частности, если в прямой задаче только два ограничения (m=2) (и сколько угодно переменных), то в двойственной задаче будет только две переменные и ее можно решить графически. После этого с использованием свойств пары двойственных задач легко найти решение исходной задачи (что и будет проделано нами позже в упражнениях).

Главное же, теория двойственности позволяет провести анализ задачи ЛП на чувствительность к изменениям исходных данных, провести т. н. постмодельный анализ полученного решения.

Пример.Построим задачу ЛП, двойственную к следующей:

3x₁ + 4x₂ – 7x₃ ≤ -9

2x₂ + 5x₃ ≤ 12

4x₁ + 15x₃ ≤ 16

x₁, x_2, x₃ ≥ 0

Z = 2x₁ – 17x₂ + 4x₃ → max.

Выпишем расширенную матрицу исходной задачи (включающую столбец правой части ограничений и строку коэффициентов целевой функции). Транспонируем ее. Получим расширенную матрицу для двойственной задачи, по которой легко построить задачу (D).

3 4 -7 -9 3 0 4 2

0 2 5 12 çè 4 2 0 -17

4 0 15 16 -7 5 15 4

2 -17 4 Z àmax -9 12 16 Fàmin

Двойственнаязадача имеет вид:

3y₁ + 4y₃ ≥ 2

4y₁ + 2y₂ ≥ -17

-7y₁ + 5y₂ + 15y₃ ≥ 4

y₁ ,y₂ ,y₃ ≥0

F = -9y₁ + 12y₂ + 16y₃ → min

Основная лемма: Если x и y – допустимые решения прямой (Р) и двойственной (D) задач, то всегда справедливо соотношение: